题目内容
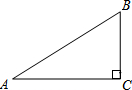在Rt△ABC中，∠C=90°，AB=10，tanA=| 3 |
| 4 |
| A、3 | B、4 | C、6 | D、8 |
考点：锐角三角函数的定义,勾股定理
专题：
分析：根据锐角三角函数正切等于对边比邻边，可得BC与AC的关系，根据勾股定理，可得AC的长．
解答：解：由tanA=
=
，得
BC=3x，CA=4x，
由勾股定理，得
BC2+AC2=AB2，即（3x）2+（4x）2=100，
解得x=2，
AC=4x=4×2=8．
故选：D．
| 3 |
| 4 |
| BC |
| AC |
BC=3x，CA=4x，
由勾股定理，得
BC2+AC2=AB2，即（3x）2+（4x）2=100，
解得x=2，
AC=4x=4×2=8．
故选：D．
点评：本题考查了锐角三角函数，利用了锐角三角函数正切等于对边比邻边，还利用了勾股定理．
练习册系列答案
阅读快车系列答案
相关题目
如图，∠ABC=∠EAC=90°，BC长为3cm，AB长为4cm，AE为12cm，求正方形CDFE的面积．
如图所示，推理填空．已知线段AB=3cm，延长线段AB到C，使BC=4cm，延长线段BA到D，使AD=AC，则线段CD的长为（ ）
| A、14cm | B、8cm |
| C、7cm | D、6cm |
如图，已知?ABCD，过A作AM⊥BC于M，交BD于E，过C作CN⊥AD于N，交BD于F，连结AF、CE．求证：四边形AECF为平行四边形．
如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使得点A′恰好落在AB上，则旋转角度为（ ）| A、60° | B、30° |
| C、90° | D、150° |
在正方形网格中，△ABC的位置如图所示，则tanB的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知，如图，圆O的弦AB=AD，∠BOD=124°，点C在劣弧 |
| BD |
| A、59° | B、62° |
| C、56° | D、42° |
让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则两个数的和是2的倍数或3的倍数的概率等于