题目内容
16．在一个不透明的袋子中装有除颜色外完全相同的3个红球、3个黄球、2个绿球，任意摸出一球，摸到红球的概率是$\frac{3}{8}$．分析 根据随机事件A的概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数，用红球的个数除以总个数，求出恰好摸到红球的概率是多少即可．
解答 解：∵袋子中共有8个球，其中红球有3个，
∴任意摸出一球，摸到红球的概率是$\frac{3}{8}$，
故答案为：$\frac{3}{8}$．
点评 此题主要考查了概率公式的应用，要熟练掌握，解答此题的关键是要明确：随机事件A的概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数．
练习册系列答案
相关题目
如图，在△ABC中，∠ACB=90°，AC=2.8，BC=2.1，则高CD=1.68．
4．下列四个数中最大的数是（ ）
| A． | 0 | B． | -1 | C． | -2 | D． | -3 |
11．
如图，一艘轮船在A处测得灯塔P位于其北偏东60°方向上，轮船沿正东方向航行30海里到达B处后，此时测得灯塔P位于其北偏东30°方向上，此时轮船与灯塔P的距离是（ ）
如图，一艘轮船在A处测得灯塔P位于其北偏东60°方向上，轮船沿正东方向航行30海里到达B处后，此时测得灯塔P位于其北偏东30°方向上，此时轮船与灯塔P的距离是（ ）| A． | 15$\sqrt{3}$海里 | B． | 30海里 | C． | 45海里 | D． | 30$\sqrt{3}$海里 |
1．下列各运算中，计算正确的是（ ）
| A． | （x-2）2=x2-4 | B． | （3a2）3=9a6 | C． | x6÷x2=x3 | D． | x3•x2=x5 |
8．点P（-3，1）在双曲线y=$\frac{k}{x}$上，则k的值是（ ）
| A． | -3 | B． | 3 | C． | $-\frac{1}{3}$ | D． | $\frac{1}{3}$ |
12．《九章算术》是我国古代的数学名著，书中的“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺．问折者高几何？意思是：一根竹子，原高一丈（一丈=10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部3尺远，问折断处离地面的高度是多少？设折断后离地面的高度为x尺，则可列方程为（ ）
| A． | x2-3=（10-x）2 | B． | x2-32=（10-x）2 | C． | x2+3=（10-x）2 | D． | x2+32=（10-x）2 |
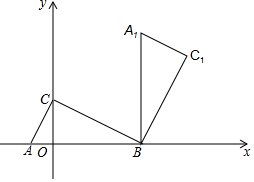如图，在平面直角坐标系中，△ABC三个顶点坐标分别为A（-1，0）、B（4，0）、C（0，2），将△ABC绕点B顺时针旋转90°得到△A1BC1，有一条抛物线经过点A，且它的顶点为A1．