题目内容
11. 阅读下列材料并解决后面的问题.
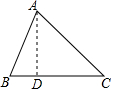
阅读下列材料并解决后面的问题.材料一:在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图),则sinB=$\frac{AD}{c}$,sinC=$\frac{AD}{b}$,即AD=csinB,AD=bsinC,于是csinB=bsinC,即$\frac{b}{sinB}$=$\frac{c}{sinC}$.同理有:$\frac{c}{sinC}$=$\frac{a}{sinA}$,$\frac{a}{sinA}$=$\frac{b}{sinB}$,所以 $\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$…(※).
即在一个三角形中,各边和它所对角的正弦的比相等,同样地,我们还可以证明在任意的三角形中,上述结论也成立.
材料二:在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,△ABC的外接圆半径为R,则 $\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R.
问题:已知a,b,c分别为△ABC的角A,B,C的对应边,
①(b+c):(a+c):(a+b)=4:5:6,则sinA:sinB:sinC=7:5:3;
②若A=60°,a=$\sqrt{3}$,则$\frac{a+b+c}{sinA+sinB+sinC}$=2;
③若bcosA=acosB,判断△ABC是等腰三角形.
分析 ①先根据已知条件得出a=7k,b=5k,c=3k,再用材料二的结论即可得出结论;
②先根据材料二得出R=1,再用等比定理即可得出结论;
③根据正弦定理即可得出结论.
解答 解:①∵(b+c):(a+c):(a+b)=4:5:6,
∴$\frac{b+c}{4}=\frac{a+c}{5}=\frac{a+b}{6}$=2k,
∴b+c=4k,a+c=5k,a+b=6k,
∴a=7k,b=5k,c=3k,
∵$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$.
∴$\frac{7k}{sinA}=\frac{5k}{sinB}=\frac{3k}{sinC}$,
∴sinA:sinB:sinC=7:5:3.
故答案为:7:5:3;
②∵A=60°,a=$\sqrt{3}$,
∴$\frac{a}{sinA}=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2=2R,
∴R=1,
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{a+b+c}{sinA+sinB+sinC}$=2R=2,
故答案为:2;
③∵bcosA=acosB,
∴由正弦定理得,sinAcosB=sinBcosA,
∴sinAcosB-sinBcosA=sin(A-B)=0,
由三角形的内角和的范围得,A=B
∴△ABC是等腰三角形,
故答案为:等腰.
点评 此题是材料题,主要考查学生的阅读能力,等比的性质,解本题的关键读懂材料,借助已学知识解决问题.

练习册系列答案
相关题目
2.在△ABC中,∠C=90°,AC=16,sinB=0.8,则BC的长是( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
19.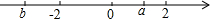 在数轴上,a,b所表示的数如图所示,下列结论正确的是( )
在数轴上,a,b所表示的数如图所示,下列结论正确的是( )
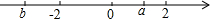 在数轴上,a,b所表示的数如图所示,下列结论正确的是( )
在数轴上,a,b所表示的数如图所示,下列结论正确的是( )| A. | a+b>0 | B. | |b|<|a| | C. | a-b>0 | D. | a•b>0 |
6.2015年7月,第四十五届“世界超强计算机500强排行榜”榜单发布,我国国防科技大学研制的“天河二号”以每秒3386×1013次的浮点运算速度第五次蝉联冠军,若将3386×1013用科学记数法表示成a×10n的形式,则n的值是( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
16.截至2015年5月7日,国内美拍用户总数超过1.4亿,日活跃用户数达1431万.美拍用户数据的快速增长,印证了短视频社交市场规模在持续扩大.1431万用科学记数法表示为( )
| A. | 1.431×106 | B. | 14.31×106 | C. | 1.431×107 | D. | 0.1431×108 |