题目内容
1.已知当1≤x≤20且x为整数时,二次函数y=-$\frac{1}{2}$x2+(14+2a)t+480-96a随着x的增大而增大,则a的取值范围为a≥-17.分析 根据解析式可求得其开口方向及对称轴,再结合条件可求得关于a的不等式组,可求得a的取值范围.
解答 解:
∵y=-$\frac{1}{2}$x2+(14+2a)t+480-96a,
∴抛物线开口向下,对称轴为x=-$\frac{14+2a}{2×(-\frac{1}{2})}$=-14-2a,
∵当1≤x≤20且x为整数时,y随着x的增大而增大,
∴20≤-14-2a,解得a≥-17,
故答案为:a≥-17.
点评 本题主要考查二次函数的性质,掌握二次函数的对称轴及开口方向及增减性是解题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
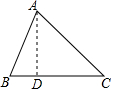
16. 如图,已知∠1=∠2,要使△ABD≌△ACD,还需从下列条件中补选一个,错误的是( )
如图,已知∠1=∠2,要使△ABD≌△ACD,还需从下列条件中补选一个,错误的是( )
 如图,已知∠1=∠2,要使△ABD≌△ACD,还需从下列条件中补选一个,错误的是( )
如图,已知∠1=∠2,要使△ABD≌△ACD,还需从下列条件中补选一个,错误的是( )| A. | ∠B=∠C | B. | DC=BD | C. | ∠3=∠4 | D. | AC=AB |
 阅读下列材料并解决后面的问题.
阅读下列材料并解决后面的问题. 如图所示,在3×3正方形网格中,已有三个小正方形被涂黑,将剩余的白色小正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有( )
如图所示,在3×3正方形网格中,已有三个小正方形被涂黑,将剩余的白色小正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有( )