题目内容
17.解下列方程:(1)2x2-3x=0;
(2)x2-4$\sqrt{2}$x+8=0;
(3)3x(x-1)=2(1-x).
分析 (1)利用因式分解法解方程;
(2)利用配方法得到(x-2$\sqrt{2}$)2=0,然后利用直接开平方法解方程;
(3)先移项得到3x(x-1)+2(x-1)=0,然后利用因式分解法解方程.
解答 解:(1)x(2x-3)=0,
x=0或2x-3=0,
所以x1=0,x2=$\frac{3}{2}$;
(2)x2-4$\sqrt{2}$x+(2$\sqrt{2}$)2=0,
(x-2$\sqrt{2}$)2=0,
所以x1=x2=2$\sqrt{2}$;
(3)3x(x-1)+2(x-1)=0,
(x-1)(3x+2)=0,
x-1=0或3x+2=0,
所以x1=1,x2=-$\frac{2}{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目
5.若(m-2)x|2m-3|=6是一元一次方程,则m的值为( )
| A. | 2 | B. | 2或1 | C. | 1 | D. | 不能确定 |
 如图,所有正方形的中心均在坐标原点O,且各边均与x轴成y轴平行,从内到外,它们的边长依次是2,4,6,8,…,每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4,A5,A6,A7,A8;…,则顶点A10的坐标为(-3,3).
如图,所有正方形的中心均在坐标原点O,且各边均与x轴成y轴平行,从内到外,它们的边长依次是2,4,6,8,…,每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4,A5,A6,A7,A8;…,则顶点A10的坐标为(-3,3).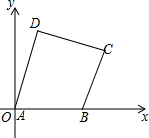 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7)
如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7) 如图,两条公路0A和0B相交于点0,在∠A0B的内部有工厂C和D.现要修建一个货站P到两条公路0A、0B的距离相等,且到两工厂C、D的距离相等.用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
如图,两条公路0A和0B相交于点0,在∠A0B的内部有工厂C和D.现要修建一个货站P到两条公路0A、0B的距离相等,且到两工厂C、D的距离相等.用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)