题目内容
已知关于x的一元二次方程x2+ax=2-a.
(1)求证:方程有两个不相等的实数根;
(2)若α、β是方程x2+ax=2-a的两个根,且α-α•β+β<0,求满足α的最小整数.
(1)求证:方程有两个不相等的实数根;
(2)若α、β是方程x2+ax=2-a的两个根,且α-α•β+β<0,求满足α的最小整数.
考点:根的判别式,根与系数的关系
专题:
分析:(1)通过一元二次方程的根的判别式负号来判定该方程的根的情况;
(2)根据根与系数的关系求得α+β、αβ的值,然后代入列出不等式,进行解答即可.
(2)根据根与系数的关系求得α+β、αβ的值,然后代入列出不等式,进行解答即可.
解答:(1)证明:由原方程,得
x2+ax-2+a=0,
则△=a2-4(-2+a)=(a+2)2+4.
∵(a+2)2≥0,
∴(a+2)2+4>0,
∴方程有两个不相等的实数根;
(2)∵α、β是方程x2+ax-2+a=0的两个根,
∴α+β=-a,α•β=-2+a,
∴由α-α•β+β<0,得
-a+2-a<0,
解得 a>2,
∴a的最小正整数是3.
x2+ax-2+a=0,
则△=a2-4(-2+a)=(a+2)2+4.
∵(a+2)2≥0,
∴(a+2)2+4>0,
∴方程有两个不相等的实数根;
(2)∵α、β是方程x2+ax-2+a=0的两个根,
∴α+β=-a,α•β=-2+a,
∴由α-α•β+β<0,得
-a+2-a<0,
解得 a>2,
∴a的最小正整数是3.
点评:本题考查了根的判别式,根与系数的关系.在解不等式时一定要注意数值的正负与不等号的变化关系.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
下列平面图形经过折叠后,不能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |
下列各式:x+1,a≠0,-a,9>2,
,S=
ab,0,其中代数式的个数是( )
| x-y |
| x+y |
| 1 |
| 2 |
| A、5 | B、4 | C、3 | D、2 |
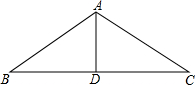 已知△ABC中,AB=17cm,BC=30cm,BC上的中线AD=8cm,请你判断△ABC的形状,并说明理由.
已知△ABC中,AB=17cm,BC=30cm,BC上的中线AD=8cm,请你判断△ABC的形状,并说明理由.