题目内容
10. 如图,在四边形ABCD中,对角线AC,BD交于点O,下列选项不能得到四边形ABCD是平行四边形的是( )
如图,在四边形ABCD中,对角线AC,BD交于点O,下列选项不能得到四边形ABCD是平行四边形的是( )| A. | AC=BD,OA=OC | B. | OB=OD,OA=OC | C. | AD=BC,AD∥BC | D. | △ABC≌△CDA |
分析 根据平行四边形的判定定理进行分析即可.
解答 解:A、AC=BD,OA=OC不能判定四边形ABCD是平行四边形,故此选项符合题意;
B、OB=OD,OA=OC可根据对角线互相平分的四边形是平行四边形判定四边形ABCD是平行四边形,故此选项不符合题意;
C、AD=BC,AD∥BC可根据一组对边平行且相等的四边形是平行四边形判定四边形ABCD是平行四边形,故此选项不符合题意;
D、△ABC≌△CDA可得AB=CD,AD=BC,可根据两组对边分别相等的四边形是平行四边形判定四边形ABCD是平行四边形,故此选项不符合题意;
故选:A.
点评 此题主要考查了平行四边形的判定,关键是掌握(1)两组对边分别平行的四边形是平行四边形.(2)两组对边分别相等的四边形是平行四边形.(3)一组对边平行且相等的四边形是平行四边形.(4)两组对角分别相等的四边形是平行四边形.(5)对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目
3. 如图,∠1=70°,如果CD∥BE,那么∠B的度数为( )
如图,∠1=70°,如果CD∥BE,那么∠B的度数为( )
 如图,∠1=70°,如果CD∥BE,那么∠B的度数为( )
如图,∠1=70°,如果CD∥BE,那么∠B的度数为( )| A. | 70° | B. | 110° | C. | 100° | D. | 120° |
1.下列数据不能确定物体位置的是( )
| A. | C区3号 | B. | 上新街2号 | ||
| C. | 东经108度、北纬30度 | D. | 北偏西60度 |
18.某校在“6.26国际禁毒月”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如下频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题

(1)表中a=12,b=0.2,并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段60≤x<70对应扇形的圆心角度数是72°;
(3)请估计该年级分数在80≤x<100的学生有多少人?
| 少分数段(x表示分数) | 频数 | 频率 |
| 50≤x<60 60≤x<70 70≤x<80 | 4 8 A | 0.1 B 0.3 |
| 80≤x<90 | 10 | 0.25 |
| 90≤x<100 | 6 | 0.15 |

(1)表中a=12,b=0.2,并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段60≤x<70对应扇形的圆心角度数是72°;
(3)请估计该年级分数在80≤x<100的学生有多少人?
15.下列命题为假命题的是( )
| A. | 一角为36°的等腰三角形中必有一个角是72° | |
| B. | 等腰三角形两底角的平分线相等 | |
| C. | 有一个角等于60°的等腰三角形是等边三角形 | |
| D. | 等腰三角形底边上的高与顶角的角平分线重合 |
2. 如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转99次后顶点A在整个旋转过程中所经过的路程之和是( )
如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转99次后顶点A在整个旋转过程中所经过的路程之和是( )
 如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转99次后顶点A在整个旋转过程中所经过的路程之和是( )
如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转99次后顶点A在整个旋转过程中所经过的路程之和是( )| A. | 288π | B. | 294π | C. | 300π | D. | 396π |
19. 如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB=$\sqrt{3}$,∠EFA=60°,则四边形A′B′EF的周长是( )
如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB=$\sqrt{3}$,∠EFA=60°,则四边形A′B′EF的周长是( )
 如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB=$\sqrt{3}$,∠EFA=60°,则四边形A′B′EF的周长是( )
如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB=$\sqrt{3}$,∠EFA=60°,则四边形A′B′EF的周长是( )| A. | 1+3$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 4+$\sqrt{3}$ | D. | 5+$\sqrt{3}$ |
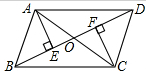 如图,在平行四边形ABCD中,对角线AC.BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:OE=OF.
如图,在平行四边形ABCD中,对角线AC.BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:OE=OF. 如图,在?ABCD中,AM⊥BC,AN⊥CD,M、N分别为垂足,∠MAN=30°,AM=5cm,AN=3cm,求?ABCD的周长.
如图,在?ABCD中,AM⊥BC,AN⊥CD,M、N分别为垂足,∠MAN=30°,AM=5cm,AN=3cm,求?ABCD的周长.