题目内容
15.一元二次方程:M:ax2+bx+c=0; N:cx2+bx+a=0,其中ac≠0,a≠c,以下四个结论:①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果方程M有两根符号相同,那么方程N的两根符号也相同;
③如果m是方程M的一个根,那么$\frac{1}{m}$是方程N的一个根;
④如果方程M和方程N有一个相同的根,那么这个根必是x=1
正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用根的判别式与求根公式直接判断①②;利用代入的方法判断③④即可.
解答 解:①两个方程根的判别式都是△=b2-4ac,所以如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根正确;
②如果方程M的两根符号相同,那么方程N的两根符号也相同,那么△=b2-4ac≥0,$\frac{c}{a}$>0,所以a与c符号相同,$\frac{a}{c}$>0,所以方程N的两根符号也相同,结论正确;
③如果m是方程M的一个根,那么m2a+mb+c=0,两边同时除以m2,得$\frac{1}{{m}^{2}}$c+$\frac{1}{m}$b+a=0,所以$\frac{1}{m}$是方程N的一个根,结论正确;
D、如果方程M和方程N有一个相同的根,那么ax2+bx+c=cx2+bx+a,(a-c)x2=a-c,由a≠c,得x2=1,x=±1,结论错误.
正确的是①②③共3个.
故选:C.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
10.花生的出油率是38%,要榨190千克的花生油需要( )千克花生仁.
| A. | 500 | B. | 600 | C. | 650 | D. | 700 |
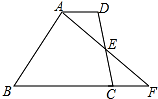 如图,在四边形ABCD中,AD∥BC,E为CD中点,连接AE并延长交BC的延长线于点F.
如图,在四边形ABCD中,AD∥BC,E为CD中点,连接AE并延长交BC的延长线于点F.