题目内容
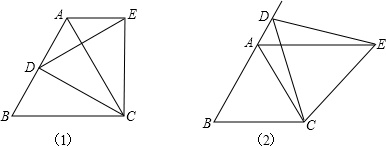
5.如图(1),等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.(1)求证:AE∥BC;
(2)如图(2),将(1)中的动点D运动到边BA的延长线上,仍作等边△EDC,请问是否仍有AE∥BC?证明你的猜想.
分析 (1)证明△ACE≌△BCD推出∠ACB=∠EAC即可证.
(2)证明△DBC≌△EAC可推出∠EAC=∠ACB,由此可证.
解答 解:(1)证明:∵∠ACB=60°,∠DCE=60°,
∴∠BCD=60°-∠ACD,∠ACE=60°-∠ACD,
∴∠BCD=∠ACE,
在△DBC和△EAC中,
∵$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=EC}\end{array}\right.$,
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60°.
又∵∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC.
(2)结论:AE∥BC,
理由:∵△ABC、△EDC为等边三角形
∴BC=AC,DC=CE,∠BCA=∠DCE=60°
∠BCA+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△DBC和△EAC中,
∵$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=EC}\end{array}\right.$,
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60°,
又∵∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC.
点评 本题考查的是全等三角形的判定和性质.关键是证明△ACE≌△BCD.

练习册系列答案
相关题目
16. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )| A. | 52° | B. | 38° | C. | 42° | D. | 60° |
13. 如图,为估计假山A、B两端的距离,小明在一侧选取了一点C,测得AC=18m,BC=12m,那么AB之间的距离不可能是( )
如图,为估计假山A、B两端的距离,小明在一侧选取了一点C,测得AC=18m,BC=12m,那么AB之间的距离不可能是( )
 如图,为估计假山A、B两端的距离,小明在一侧选取了一点C,测得AC=18m,BC=12m,那么AB之间的距离不可能是( )
如图,为估计假山A、B两端的距离,小明在一侧选取了一点C,测得AC=18m,BC=12m,那么AB之间的距离不可能是( )| A. | 12m | B. | 16m | C. | 18m | D. | 30m |
10.下列各式去括号正确的是( )
| A. | a-(b-c)=a-b-c | B. | a+(b-c)=a+b-c | ||
| C. | a2-(a-b+c)=a2-a-b+c | D. | a+2(3a-5)=a+6a-5 |
15.一辆汽车在a s内行驶m m,则它在2min内行驶的路程为( )
| A. | $\frac{m}{3}$m | B. | $\frac{20m}{a}$m | C. | $\frac{10a}{a}$m | D. | $\frac{120m}{a}$m |
 如图,在△ABC中,∠ABC,∠ACB的角平分线相交于点O,过点O作DE∥BC分别交AB、AC于D、E两点,AB=6,AC=8,则△ADE的周长是14.
如图,在△ABC中,∠ABC,∠ACB的角平分线相交于点O,过点O作DE∥BC分别交AB、AC于D、E两点,AB=6,AC=8,则△ADE的周长是14.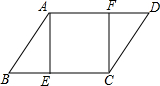 如图,在?ABCD中,∠B=60°,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,BC=2+2$\sqrt{3}$,则AB的长为( )
如图,在?ABCD中,∠B=60°,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,BC=2+2$\sqrt{3}$,则AB的长为( )