题目内容
20.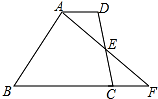 如图,在四边形ABCD中,AD∥BC,E为CD中点,连接AE并延长交BC的延长线于点F.
如图,在四边形ABCD中,AD∥BC,E为CD中点,连接AE并延长交BC的延长线于点F.(1)求证:CF=AD;
(2)连接BE,若BE⊥AF,AD=2,AB=6,求BC的长.
分析 (1)根据AAS证明△ADE与△FCE全等即可;
(2)根据全等三角形的性质解答即可.
解答 证明:(1)∵AD∥BC,
∴∠DAE=∠CFE,∠D=∠ECF,
∵E为CD的中点,
∴DE=CE,
在△ADE与△FCE中,
$\left\{\begin{array}{l}{∠DAE=∠CFE}\\{∠D=∠ECF}\\{DE=CE}\end{array}\right.$,
∴△ADE≌△FCE(AAS),
∴CF=AD;
(2)∵△ADE≌△FCE,
∴CF=AD=2,AE=EF,
∵BE⊥AF,
∴BF=AB=6,
∴BC=BF-CF=6-2=4.
点评 此题主要考查全等三角形的判定和性质,关键是根据AAS证明△ADE与△FCE全等.

练习册系列答案
相关题目
8.下列说法正确的是( )
| A. | 0是最小的有理数 | |
| B. | 一个有理数不是正数,就是负数 | |
| C. | 在数轴上0与-1之间没有负数 | |
| D. | 所有的有理数都可以在数轴上表示出来 |
5.绝对值大于2而小于5的所有整数的积是( )
| A. | 144 | B. | -144 | C. | 14400 | D. | -14400 |
10.下列各式去括号正确的是( )
| A. | a-(b-c)=a-b-c | B. | a+(b-c)=a+b-c | ||
| C. | a2-(a-b+c)=a2-a-b+c | D. | a+2(3a-5)=a+6a-5 |
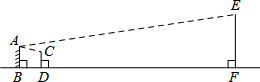 如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为7m.
如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为7m.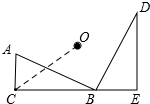 如图,将Rt△ABC绕O点旋转90°,得Rt△BDE,其中∠ACB=∠BED=90°,AC=6,AB=10,则点C与旋转中心点O的距离OC的长是7$\sqrt{2}$.
如图,将Rt△ABC绕O点旋转90°,得Rt△BDE,其中∠ACB=∠BED=90°,AC=6,AB=10,则点C与旋转中心点O的距离OC的长是7$\sqrt{2}$.