题目内容
6.在一个不透明的口袋中放有4个完全相同的小球,他们分别标有数字-1,2,3,5.小明先随机摸出一个小球,记下数字为x;小强再随机摸出一个小球,记下数字为y.小明小强共同商议游戏规则为:当x>y时小明获胜,否则小强获胜.(1)若小明摸出的球不放回,请用列表或画树状图的方法求小明获胜的概率;
(2)若小明摸出的球放回后小强再随机摸球,请问这个游戏规则是公平的吗?请说明理由.
分析 (1)通过列表展示所有12种等可能性的结果数,即可求出小明获胜的概率;
(2)游戏是否公平,求出游戏双方获胜的概率,比较是否相等即可.
解答 解:(1)根据题意,列表如下:
| 小明摸出的x小强摸出的y | -1 | 2 | 3 | 5 |
| -1 | / | (2,-1) | (3,-1) | (5,-1) |
| 2 | (-1,2) | / | (3,2) | (5,2) |
| 3 | (-1,3) | (2,3) | / | (5,3) |
| 5 | (-1,5) | (2,5) | (3,5) | / |
∴P(小明获胜)=$\frac{6}{12}=\frac{1}{2}$;
(2)不公平,理由如下:
由题意,列表为:
| 小明摸出的x小强摸出的y | -1 | 2 | 3 | 5 |
| -1 | (-1,-1) | (2,-1) | (3,-1) | (5,-1) |
| 2 | (-1,2) | (2,2) | (3,2) | (5,2) |
| 3 | (-1,3) | (2,3) | (3,3) | (5,3) |
| 5 | (-1,5) | (2,5) | (3,5) | (5,5) |
∴P(小明获胜)=$\frac{6}{16}=\frac{3}{8}$,
P(小强获胜)=1-$\frac{3}{8}$=$\frac{5}{8}$,
P(小明获胜)<P(小强获胜)
∴游戏规则不公平.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
16.化简$\sqrt{-x{y}^{2}}$(y<0)的结果是( )
| A. | y$\sqrt{x}$ | B. | y$\sqrt{-x}$ | C. | -y$\sqrt{x}$ | D. | -y$\sqrt{-x}$ |
16. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )| A. | 52° | B. | 38° | C. | 42° | D. | 60° |
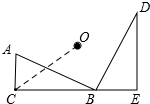 如图,将Rt△ABC绕O点旋转90°,得Rt△BDE,其中∠ACB=∠BED=90°,AC=6,AB=10,则点C与旋转中心点O的距离OC的长是7$\sqrt{2}$.
如图,将Rt△ABC绕O点旋转90°,得Rt△BDE,其中∠ACB=∠BED=90°,AC=6,AB=10,则点C与旋转中心点O的距离OC的长是7$\sqrt{2}$.