题目内容
 如图,已知菱形ABCD中,AC=8cm,BD=6cm,求菱形ABCD的周长和面积.
如图,已知菱形ABCD中,AC=8cm,BD=6cm,求菱形ABCD的周长和面积.考点:菱形的性质
专题:
分析:由菱形ABCD中,AC=8cm,BD=6cm,根据菱形的性质可得:AC⊥BD,OA=
AC=4cm,OB=
BD=3cm,然后由勾股定理求得AB的长,继而求得菱形ABCD的周长和面积.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵四边形ABCD是菱形,AC=8cm,BD=6cm,
∴AC⊥BD,OA=
AC=4cm,OB=
BD=3cm,
∴AB=
=5(cm),
∴菱形ABCD的周长为:5×4=20(cm);
面积为:
AC•BD=
×8×6=24(cm2).
∴AC⊥BD,OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| OA2+OB2 |
∴菱形ABCD的周长为:5×4=20(cm);
面积为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了菱形的性质与勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目

 如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=
如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=
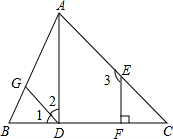 如图,已知EF⊥BC,∠1=∠C,∠2+∠3=180°.试说明直线AD与BC垂直(请在下面的解答过程的空格内填空或在括号内填写理由)
如图,已知EF⊥BC,∠1=∠C,∠2+∠3=180°.试说明直线AD与BC垂直(请在下面的解答过程的空格内填空或在括号内填写理由) 如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).