题目内容
3.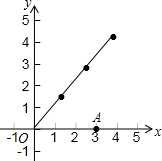 如图,在平面直角坐标系中,A点坐标为(3,0),线段OA绕原点O每次按逆时针方向旋转60°,并且每旋转一次长度增加两倍,例如:OA1=3OA,∠A1OA=60°,那么按照此规律,A2的坐标为(-$\frac{27}{2}$,$\frac{27\sqrt{3}}{2}$),A100的坐标为$(-\frac{{3}^{101}}{2},-\frac{{3}^{101}\sqrt{3}}{2})$.
如图,在平面直角坐标系中,A点坐标为(3,0),线段OA绕原点O每次按逆时针方向旋转60°,并且每旋转一次长度增加两倍,例如:OA1=3OA,∠A1OA=60°,那么按照此规律,A2的坐标为(-$\frac{27}{2}$,$\frac{27\sqrt{3}}{2}$),A100的坐标为$(-\frac{{3}^{101}}{2},-\frac{{3}^{101}\sqrt{3}}{2})$.
分析 根据题意可得每次旋转后OAn的长度,由线段OA绕原点O每次按逆时针方向旋转60°判断出每转六次正好转一圈,可以判断出点An所在的象限,从而可以解答本题.
解答 解:∵在平面直角坐标系中,A点坐标为(3,0),线段OA绕原点O每次按逆时针方向旋转60°,每旋转一次长度增加两倍,
∴$O{A}_{1}=3OA=3×3={3}^{2}$,$O{A}_{2}=3O{A}_{1}={3}^{3}$.
∵线段OA绕原点O每次按逆时针方向旋转60°,
∴点A2在第二象限.
∴A2的坐标为:($-\frac{{3}^{3}}{2},\frac{{3}^{3}\sqrt{3}}{2}$).
即A2的坐标为:$(-\frac{27}{2},\frac{27\sqrt{3}}{2})$.
∵线段OA绕原点O每次按逆时针方向旋转60°,
∴OA旋转6次正好转一圈.
∵100÷6=16…4,
∴第100次,点A100在第三象限.
∴A100的坐标为:$(-\frac{{3}^{101}}{2},-\frac{{3}^{101}\sqrt{3}}{2})$.
故答案为:$(-\frac{27}{2},\frac{27\sqrt{3}}{2})$,$(-\frac{{3}^{101}}{2},-\frac{{3}^{101}\sqrt{3}}{2})$.
点评 本题考查探究点的坐标的问题,关键是找出点运动的规律,判断出点每次运动后所在的象限和每次运动后OAn的长度.

练习册系列答案
相关题目
8.用配方法解方程x2-8x+7=0,配方后正确的是( )
| A. | (x-4)2=7 | B. | (x-4)2=11 | C. | (x-4)2=9 | D. | (x+4)2=7 |
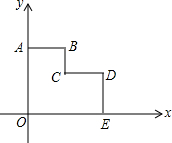 如图,在平面直角坐标系xOy中,多边形OABCDE的顶点分别为O(0,0)、A(0,8)、B(4,8)、C(4,4)、D(8,4)、E(8,0),若直线l经过点M(3,$\frac{7}{2}$),分别与边OA、DE相交且将多边形OABCDE面积平分.
如图,在平面直角坐标系xOy中,多边形OABCDE的顶点分别为O(0,0)、A(0,8)、B(4,8)、C(4,4)、D(8,4)、E(8,0),若直线l经过点M(3,$\frac{7}{2}$),分别与边OA、DE相交且将多边形OABCDE面积平分.
 如图,矩形ABCD的两边BC、CD分别在x轴、y轴上,点C与原点重合,点A(-1,2),将矩形ABCD沿x轴向右翻滚,经过一次翻滚点A对应点记为A1,经过第二次翻滚点A对应点记为A2…依此类推,经过5次翻滚后点A对应点A5的坐标为( )
如图,矩形ABCD的两边BC、CD分别在x轴、y轴上,点C与原点重合,点A(-1,2),将矩形ABCD沿x轴向右翻滚,经过一次翻滚点A对应点记为A1,经过第二次翻滚点A对应点记为A2…依此类推,经过5次翻滚后点A对应点A5的坐标为( )