题目内容
2.抛物线y=x2+x的顶点坐标是(-$\frac{1}{2}$,-$\frac{1}{4}$),y的最小值=-$\frac{1}{4}$.分析 先把函数解析式配成顶点式得到y=(x+$\frac{1}{2}$)2-$\frac{1}{4}$,然后根据顶点式即可得到顶点坐标,进一步得出最值即可.
解答 解:∵y=x2+x=(x+$\frac{1}{2}$)2-$\frac{1}{4}$,
∴顶点坐标是(-$\frac{1}{2}$,-$\frac{1}{4}$),
a>0,y的最小值=$-\frac{1}{4}$.
故答案为:(-$\frac{1}{2}$,-$\frac{1}{4}$),-$\frac{1}{4}$.
点评 本题考查了二次函数的性质,利用配方法是一种常用求顶点坐标和最值得方法.

练习册系列答案
相关题目
12.已知函数y=kx+2,当k取不同的数值时,可以得到许多不同的直线,这些直线必定是( )
| A. | 交于同一个交点 | B. | 有无数个交点 | C. | 互相平行 | D. | 互相垂直 |
17.计算:(102)3的结果是( )
| A. | 106 | B. | 108 | C. | 109 | D. | 105 |
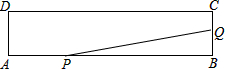 如图所示,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB边上沿AB方向以2cm/s的速度匀速运动,点Q在边BC边上沿BC方向以1cm/s的速度匀速运动,当其中一个点停止运动时,另一个点也停止运动,设运动时间为xs,△PBQ的面积为y(cm2).
如图所示,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB边上沿AB方向以2cm/s的速度匀速运动,点Q在边BC边上沿BC方向以1cm/s的速度匀速运动,当其中一个点停止运动时,另一个点也停止运动,设运动时间为xs,△PBQ的面积为y(cm2). 如图,点A,E,B,D在同一条直线上,AE=DB,∠A=∠D,∠C=∠F.试判断△ABC与△DEF是否全等,并说明理由.
如图,点A,E,B,D在同一条直线上,AE=DB,∠A=∠D,∠C=∠F.试判断△ABC与△DEF是否全等,并说明理由.