Question

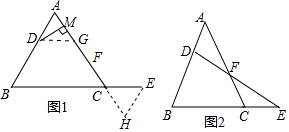
10．已知，在△ABC中，点D在AB上，点E是BC延长线上一点，且AD=CE，连接DE交AC于点F．
（1）猜想证明：如图1，在△ABC中，若AB=BC，学生们发现：DF=EF．下面是两位学生的证明思路：
思路1：过点D作DG∥BC，交AC于点G，可证△DFG≌△EFC得出结论；
思路2：过点E作EH∥AB，交AC的延长线于点H，可证△ADF≌△HEF得出结论；
…

请你参考上面的思路，证明DF=EF（只用一种方法证明即可）．
（2）类比探究：在（1）的条件下（如图1），过点D作DM⊥AC于点M，试探究线段AM，MF，FC之间满足的数量关系，并证明你的结论．
（3）延伸拓展：如图2，在△ABC中，若AB=AC，∠ABC=2∠BAC，$\frac{AB}{BC}$=m，请你用尺规作图在图2中作出AD的垂直平分线交AC于点N（不写作法，只保留作图痕迹），并用含m的代数式直接表示$\frac{NF}{AC}$的值．

Answer 1

分析 （1）思路1：过点D作DG∥BC，交AC于点G，可证△DFG≌△EFC得出结论；思路2：过点E作EH∥AB，交AC的延长线于点H，可证△ADF≌△HEF得出结论；
（2）结论：FM=AM+FC．如图2中只要证明FG=FC，AM=FM即可解决问题；
（3）连接DN．作DG∥CE交AC于G．设DG=a，BC=b，则AB=BC=mb，AD=AG=ma，由△GDN∽△GAD，推出DG²=GN•GA，易知DG=DN=AN=a，可得a²=（ma-a）•ma，即m²a-ma-a=0，由DG∥CE，推出DG：EC=FG：FC=DG：DA=1：m，由CG=mb-ma，推出FG=$\frac{1}{m+1}$m（b-a），推出FN=GN+FG=ma-a+$\frac{1}{m+1}$m（b-a）=$\frac{mb}{m+1}$，由此即可解决问题；

解答 解：（1）思路1：如图1-1中，过点D作DG∥BC，交AC于点G．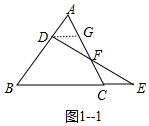

∵BA=BC，
∴∠A=∠BCA，
∵DG∥BC，
∴∠DGA=∠BCA，∠DGF=∠ECF，
∴∠A=∠DGA，
∴DA=DG，
∵AD=CE，
∴DG=CE，
∵∠DFG=∠CFE，
∴△DFG≌△EFC，
∴DF=EF．
思路2：如图1-2中，过点E作EH∥AB，交AC的延长线于点H．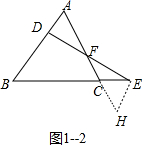

∵BA=BC，
∴∠A=∠BCA，
∵EH∥AB，
∴∠A=∠H，∠ECH=∠BCA，
∴∠H=∠ECH，
∴EC=EH，
∵AD=CE，
∴AD=EH，
∵∠AFD=∠EFH，
∴△DFA≌△EFH，
∴DF=EF．

（2）结论：FM=AM+FC．
理由：如图2中，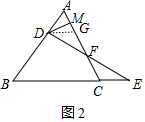

由思路1可知：DA=DG，△DFG≌△EFC，
∵DM⊥AG，
∴AM=FG，FG=FC，
∵FM=FG+GM，
∴FM=AM+FC．

（3）AD的垂直平分线交AC于点N，如图3中所示．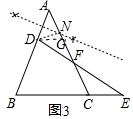

连接DN．作DG∥CE交AC于G．设DG=a，BC=b，则AB=BC=mb，AD=AG=ma，
∵∠ABC=2∠BAC，设∠BAC=x，则∠B=∠ACB=2x，
∴5x=180°，
∴x=36°，
∴∠A=30°，
∵NA=ND，
∴∠A=∠ADN=36°，
∵∠ADG=∠B=72°，
∴∠NDG=∠A=36°，∵∠DGN=∠AGD，
∴△GDN∽△GAD，
∴DG²=GN•GA，
易知DG=DN=AN=a，
∴a²=（ma-a）•ma，
∴m²a-ma-a=0，
∵DG∥CE，
∴DG：EC=FG：FC=DG：DA=1：m，
∵CG=mb-ma，
∴FG=$\frac{1}{m+1}$m（b-a），
∴FN=GN+FG=ma-a+$\frac{1}{m+1}$m（b-a）=$\frac{{m}^{2}a-a+mb-ma}{m+1}$=$\frac{mb}{m+1}$，
∴$\frac{FN}{AC}$=$\frac{\frac{mb}{m+1}}{mb}$=$\frac{1}{m+1}$．

点评 本题考查相似形综合题、全等三角形的判定和性质、等腰三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数解决问题，属于中考压轴题．