当m≠3时.方程mx2-2x+5=3x2是一元二次方程．题目和参考答案——青夏教育精英家教网—

题目内容

7．当m≠3时，方程mx²-2x+5=3x²是一元二次方程．

分析根据一元二次方程的定义，一元二次方程必须满足两个条件：未知数的最高次数是2；二次项系数不为0．由这两个条件得到相应的关系式，再求解即可．

解答解：化简，得
（m-3）x²-2x+5=0．
由题意，得
m-3≠0，
解得m≠3，
故答案为：3．

点评本题利用了一元二次方程的概念．只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程，一般形式是ax²+bx+c=0（且a≠0）．特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．

练习册系列答案

相关题目

17．

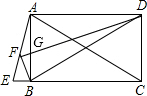已知四边形ABCD为矩形，延长CB到E，使CE=CA，连接AE，F为AE的中点，连接BF，DF，DF交AB于点G，下列结论：
（1）BF⊥DF；
（2）S_△BDG=S_△ADF；
（3）EF²=FG•FD；
（4）$\frac{AG}{BG}$=$\frac{BC}{AC}$
其中正确的个数是（　　）

18．

如图，AD为△ABC的中线，E为AD的中点，若△ABE的面积为15，则△ABC的面积为60．

15．定义：如果二次函数y=a₁x²+b₁x+c₁（a₁≠0，a₁，b₁，c₁是常数）与y=a₂x²+b₂x+c₂（a₂≠0，a₂，b₂，c₂是常数）满足a₁+a₂=0，b₁=b₂，c₁+c₂=0，则称这两个函数互为“旋转函数”．写出y=-x²+3x-2函数的“旋转函数”y=x²+3x+2．

2．如果（x²-y²）²+k=x⁴+x²y²+y⁴，则单项式k等于（　　）

-x²y²

x²y²

2x²y²

3x²y²

12．近似数1.25与1.250一样吗？为什么？

19．将129500四舍五入精确到千位得到的近似数为1.30×10⁵，它有3个有效数字．

10．将平行四边形ABCD置于平面直角坐标系中，使得边A点与坐标原点重合，AB在x轴正半轴上，AB=8，AD=4，∠BAD=60°，动点P以1个单位每秒的速度从D点出发沿DC方向运动，设运动时间为t，过P点作PQ垂直x轴，垂足为Q（当Q点与B点重合时，P点停止运动），PQ与BD交于点H，点A、D关于PQ的对称点分别为点E、F，点G为射线EF与射线DB的交点．

（1）如图1，当点G在线段BD上时，求证：△HGE∽△ABD；
（2）t为何值时，△GHF是等腰三角形；
（3）P点运动过程中，设四边形EFQH与ABCD的重合部分面积为S，求S与t的函数关系式，并写出自变量取值范围．

11．

函数y₁=2x-5和y₂=x-2的图象如图所示，若y₁＜y₂，则x的取值范围是（　　）

试题分类