题目内容
水平直线上顺次三点A、O、B,以O点为顶点在直线上方作∠COD=40°,OM、ON分别平分∠AOC和∠BOD,求∠MON的度数.
考点:角平分线的定义
专题:
分析:由OM、ON分别平分∠AOC和∠BOD,得出∠AOM=∠COM=
∠AOC,∠BON=∠DON=
∠BOD.再分两种情况进行讨论:①OD在∠AOC外部,由平角定义求出∠AOC+∠BOD=180°-40°=140°,则∠AOM+∠BON=
(∠AOC+∠BOD)=70°,于是∠MON=180°-(∠AOM+∠BON)=180°-70°=110°;②OD在∠AOC内部,由平角定义求出∠AOC+∠BOD=180°+40°=220°,则∠AOM+∠BON=
(∠AOC+∠BOD)=110°,于是∠MON=180°-(∠AOM+∠BON)=180°-110°=70°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: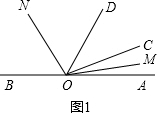 解:∵OM、ON分别平分∠AOC和∠BOD,
解:∵OM、ON分别平分∠AOC和∠BOD,
∴∠AOM=∠COM=
∠AOC,∠BON=∠DON=
∠BOD.
分两种情况:
①如图1,∵∠AOC+∠COD+∠BOD=180°,∠COD=40°,
∴∠AOC+∠BOD=180°-40°=140°,
∴∠AOM+∠BON=
∠AOC+
∠BOD=
(∠AOC+∠BOD)=
×140°=70°,
 ∴∠MON=180°-(∠AOM+∠BON)=180°-70°=110°;
∴∠MON=180°-(∠AOM+∠BON)=180°-70°=110°;
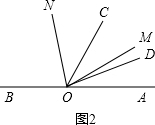
②如图2,∵∠AOC-∠COD+∠BOD=180°,∠COD=40°,
∴∠AOC+∠BOD=180°+40°=220°,
∴∠AOM+∠BON=
∠AOC+
∠BOD=
(∠AOC+∠BOD)=
×220°=110°,
∴∠MON=180°-(∠AOM+∠BON)=180°-110°=70°.
综上所述,∠MON的度数为110°或70°.
 解:∵OM、ON分别平分∠AOC和∠BOD,
解:∵OM、ON分别平分∠AOC和∠BOD,∴∠AOM=∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
分两种情况:
①如图1,∵∠AOC+∠COD+∠BOD=180°,∠COD=40°,
∴∠AOC+∠BOD=180°-40°=140°,
∴∠AOM+∠BON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 ∴∠MON=180°-(∠AOM+∠BON)=180°-70°=110°;
∴∠MON=180°-(∠AOM+∠BON)=180°-70°=110°;②如图2,∵∠AOC-∠COD+∠BOD=180°,∠COD=40°,
∴∠AOC+∠BOD=180°+40°=220°,
∴∠AOM+∠BON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=180°-(∠AOM+∠BON)=180°-110°=70°.
综上所述,∠MON的度数为110°或70°.
点评:本题考查了角的计算及角平分线定义,难度适中.进行分类讨论正确画出图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列图形经过折叠,能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |
下列长度的三条线段,能组成三角形的是( )
| A、1、2、3 |
| B、3、4、5 |
| C、1、4、6 |
| D、2、3、7 |
用尺规作图,不能作出唯一三角形的是( )
| A、已知两角和夹边 |
| B、已知两边和其中一边的对角 |
| C、已知两边和夹角 |
| D、已知两角和其中一角的对边 |
 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )| A、60° | B、30° |
| C、90° | D、150° |
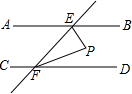 已知,如图AB∥CD,∠AEF与∠EFC的角平分线相交于点P,试说明EP⊥PF.
已知,如图AB∥CD,∠AEF与∠EFC的角平分线相交于点P,试说明EP⊥PF. 如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB.
如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB. 如图,∠ABC=∠EAC=90°,BC长为3cm,AB长为4cm,AE为12cm,求正方形CDFE的面积.
如图,∠ABC=∠EAC=90°,BC长为3cm,AB长为4cm,AE为12cm,求正方形CDFE的面积. 如图所示,已知四边形ABCD中,AB∥CD,BC⊥CD,∠A=60°,CD=
如图所示,已知四边形ABCD中,AB∥CD,BC⊥CD,∠A=60°,CD=