题目内容
下列长度的三条线段,能组成三角形的是( )
| A、1、2、3 |
| B、3、4、5 |
| C、1、4、6 |
| D、2、3、7 |
考点:三角形三边关系
专题:
分析:根据三角形的三边满足两边之和大于第三边来进行判断.
解答:解:A、1+2=3,不能构成三角形,故此选项错误;
B、3+4>5,能构成三角形,故此选项正确;
C、1+4<6,不能构成三角形,故此选项错误;
D、3+2<7,不能构成三角形,故此选项错误.
故选B.
B、3+4>5,能构成三角形,故此选项正确;
C、1+4<6,不能构成三角形,故此选项错误;
D、3+2<7,不能构成三角形,故此选项错误.
故选B.
点评:此题主要考查了三角形的三边关系,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.

练习册系列答案
相关题目
 如图的立体图形可由哪个平面图形绕轴旋转而成( )
如图的立体图形可由哪个平面图形绕轴旋转而成( )A、 |
B、 |
C、 |
D、 |
下列说法中不正确的是( )
| A、两直角边对应相等的两个直角三角形一定全等 |
| B、两个等边三角形是全等三角形 |
| C、斜边和一条直角边对应相等的两个直角三角形一定全等 |
| D、两边一角对应相等的两个三角形不一定全等 |
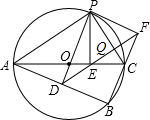 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交PC于点Q,同时交BC的延长线于F点,连接PF、PA.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交PC于点Q,同时交BC的延长线于F点,连接PF、PA. 小昆和小明玩摸牌游戏,游戏规则如下,有3张背面完全相同,牌面标有数字1、2、3的纸牌,将纸牌洗匀后背面朝上放在桌子上,随机抽出一张,记下牌面数字,再从剩下的牌中抽出一张,两次抽到的牌分别记为A、B.
小昆和小明玩摸牌游戏,游戏规则如下,有3张背面完全相同,牌面标有数字1、2、3的纸牌,将纸牌洗匀后背面朝上放在桌子上,随机抽出一张,记下牌面数字,再从剩下的牌中抽出一张,两次抽到的牌分别记为A、B. 如图,在∠1到∠6的六个角中,同位角有
如图,在∠1到∠6的六个角中,同位角有