题目内容

（1）如图a，边长为3cm，与5cm的两个正方形并排放在一起，在大正方形中画一段以它的一个顶点为圆心，边长为半径的圆弧，则阴影部分的面积是cm^2（π取3）．
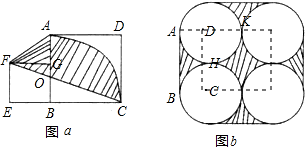
（2）如果图b中4个圆的半径都为a，那么阴影部分的面积为．

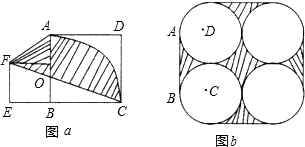
解：（1）设图a中阴影部分的面积是S，正方形EBGF的面积是S₁，以B为圆心，以BA为半径的圆的面积是S₂，△FGA的面积是S₃，△EFC的面积是S₄
则：S=S₁+S₃+ $\text{[math]}$ S₂-S₄，
∵S₁=3²=9，
S₂=π•5²=25π，
S₃= $\text{[math]}$ ×3×（5-3）=3，
S₄= $\text{[math]}$ ×（3+5）×3=12，
∴S=9+3+ $\text{[math]}$ ×25π-12，
≈18.75．
答：阴影部分的面积是 18.75cm²．

（2）连接AD DM MN CN DC CB，DM过切点K，DC过切点H，
阴影部分（1）的面积是S_矩形ADCB-2× $\text{[math]}$ S_圆，
=2a•a- $\text{[math]}$ πa²=2a²- $\text{[math]}$ πa²，
阴影部分（2）的面积是S_{正方形DCNM}-S_圆，
=2a•2a-π•a²=4a²-πa²，
所以图b的阴影部分的面积是4（2a²- $\text{[math]}$ πa²）+（4a²-πa²），
=12a²-3πa²．

分析：（1）把图形进行分割和重新组合，变不规则图形为规则图形得到阴影部分的面积S=S₁+S₃+ $\text{[math]}$ S₂-S₄，算出每个图形的面积代入即可；
（2）通过连接AD、DM、MN、CN、DC、CB，则阴影部分的面积等于S_矩形ADCB-2× $\text{[math]}$ S_圆，算出矩形和圆的面积代入即可．
点评：本题主要考查了正方形的面积，三角形的面积，圆的面积，面积和等积变形等知识点，解此题的关键是加强对图形结构的分析，寻找等积式子．