题目内容
1.化简,求值.$\frac{1}{a+1}-\frac{a+3}{{a}^{2}-1}$$•\frac{{a}^{2}-2a+1}{{a}^{2}+6a+9}$,其中a=3.分析 原式第二项约分后,两项通分并利用同分母分式的减法法则计算,得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{1}{a+1}$-$\frac{a+3}{(a+1)(a-1)}$•$\frac{(a-1)^{2}}{(a+3)^{2}}$=$\frac{1}{a+1}$-$\frac{a-1}{(a+1)(a+3)}$=$\frac{a+3-a+1}{(a+1)(a+3)}$=$\frac{4}{{a}^{2}+4a+3}$,
当a=3时,原式=$\frac{1}{6}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.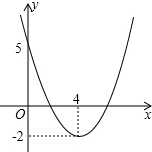 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )| A. | m≥-2 | B. | m≥5 | C. | m≥0 | D. | m>4 |
16.下列运算中错误的是( )
| A. | $\frac{a}{b}$=$\frac{a{c}^{2}}{b{c}^{2}}$ | B. | $\frac{-a-b}{a+b}$=-1 | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a}{b}$=$\frac{a({k}^{2}+1)}{b({k}^{2}+1)}$ |
6.绝对值大于3且小于6的所有整数的和是( )
| A. | 0 | B. | 9 | C. | 6 | D. | 18 |
11.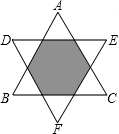 如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
 如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
