Question

13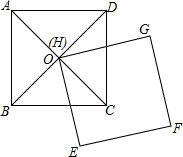．如图，已知正方形ABCD的中心为O，用纸片剪下一个大小与正方形ABCD相等的正方形EFGH，然后把正方形EFGH的顶点H固定在点O，让正方形EFGH绕点O旋转，正方形ABCD与纸片重合的部分随着纸片旋转的位置不同，而形状也会有所改变，它们有什么相同的地方吗？请你探究问题的结论
（1）旋转过程中，OD落在边HG上，那么OC应落在边HE上，重合的部分是△DOC，它的面积是正方形ABCD的面积是$\frac{1}{4}$；
（2）旋转过程中边HG⊥CD时，纸片与正方形ABCD重合部分是一个正方形；
（3）由以上两种旋转过程中特殊位置可以推测，纸片与正方形ABCD重合部分的形状会发生变化，面积会改变吗？请你总结探索的结论，并加以证明．

Answer 1

分析 （1）先根据正方形的性质可得∠DOC=∠GOE=90°，再根据旋转的性质可知旋转过程中，OD落在边HG上时，OC应落在边OE上，重合的部分是△DOC，它的面积是正方形ABCD的面积的$\frac{1}{4}$；
（2）根据旋转的性质可知旋转过程中边HG⊥CD时，HE⊥BC，易证纸片与正方形ABCD重合部分是一个正方形；
（3）由以上两种旋转过程中特殊位置可以推测，纸片与正方形ABCD重合部分的形状会发生变化，面积不会改变，是正方形ABCD的面积的$\frac{1}{4}$．理由是：由四边形ABCD，EFGH都是正方形，得到OC=OD，∠OCP=∠ODQ=45°，∠COD=∠POQ=90°，得到∠COP=∠DOQ，则△COP≌△DOQ，即可得到S_重合部分=S_△COD=$\frac{1}{4}$S_{正方形ABCD}．

解答 解：（1）如图1，旋转过程中，OD落在边HG上，那么OC应落在边HE上，重合的部分是△DOC，它的面积是正方形ABCD的面积的$\frac{1}{4}$；


（2）如图2，旋转过程中边HG⊥CD时，纸片与正方形ABCD重合部分是一个正方形；

（3）如图3，∵四边形ABCD，EFGH都是正方形，
∴OC=OD，∠OCP=∠ODQ=45°，∠COD=∠POQ=90°，
∴∠COP=∠DOQ=90°-∠COQ．
在△COP与△DOQ中，
$\left\{\begin{array}{l}{∠COP=∠DOQ}\\{OC=OD}\\{∠OCP=∠ODQ}\end{array}\right.$，
∴△COP≌△DOQ，
∴S_重合部分=S_{四边形OPCQ}=S_△COP+S_△COQ=S_△DOQ+S_△COQ=S_△COD=$\frac{1}{4}$S_{正方形ABCD}．
故答案为△DOC，$\frac{1}{4}$；正方形．

点评 本题考查了旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．也考查了正方形的性质以及三角形全等的判定与性质．