题目内容
16.若点P(2m-3n,2)、Q(-3,n-m)关于原点对称,则m+n=4.分析 根据关于原点对称的点的横坐标与纵坐标都互为相反数列方程组求出m、n的值,然后相加计算即可得解.
解答 解:∵点P(2m-3n,2)、Q(-3,n-m)关于原点对称,
∴$\left\{\begin{array}{l}{2m-3n=3}\\{n-m=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=3}\\{n=1}\end{array}\right.$,
所以,m+n=3+1=4.
故答案为:4.
点评 本题考查了关于原点对称的点的坐标,两点关于原点对称,则两点的横、纵坐标都是互为相反数.

练习册系列答案
相关题目
6.已知-1<x<0,那么在x、2x、$\sqrt{(-x)}$、-x2中最小的数是( )
| A. | -x2 | B. | 2x | C. | $\sqrt{(-x)}$ | D. | x |
 如图,已知三点A、B、C.
如图,已知三点A、B、C.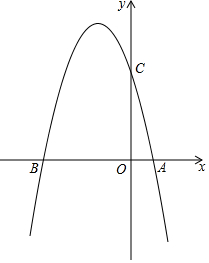 如图,已知抛物线经过A(1,0),C(0,4)两点,交x轴于另一点B,其对称轴是x=-1.5.
如图,已知抛物线经过A(1,0),C(0,4)两点,交x轴于另一点B,其对称轴是x=-1.5.