题目内容
某商场出售一批进价为3元的小工艺品,在市场营销中发现此工艺品的日销售单位x(单位:元)与日销售量y(单位:个)之间有表中关系:
(1)根据表中数据反映规律确定y与x之间的函数关系式;
(2)设经营此小工艺品的日销售利润为S元,求出S与x之间的函数关系式;
(3)物价局规定小商品的利润不得高于进价的200%,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大日销售利润是多少?
| 日销售单价x/元 | 4 | 5 | 6 | 7 |
| 日销售量y/个 | 105 | 84 | 70 | 60 |
(2)设经营此小工艺品的日销售利润为S元,求出S与x之间的函数关系式;
(3)物价局规定小商品的利润不得高于进价的200%,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大日销售利润是多少?
考点:二次函数的应用
专题:
分析:(1)利用表中数据规律可知x与y的乘积一定进而得出y与x之间的函数关系式;
(2)利用(1)中所求,再利用进价为3元,进而得出每件利润,即可得出S与x之间的函数关系式;
(3)首先得出x的取值范围,进而利用函数增减性得出答案.
(2)利用(1)中所求,再利用进价为3元,进而得出每件利润,即可得出S与x之间的函数关系式;
(3)首先得出x的取值范围,进而利用函数增减性得出答案.
解答:解:(1)由表中数据规律可知x与y的乘积一定,为105×4=420.
所以函数关系式为:y=
;
(2)根据题意可得:
S=(x-3)×
=-
+420;
(3)由题意可知:x≤3+3×200%,
∴3≤x≤9,
∵k=-1260<0,
∴S随x的增大而增大,
∴当x=9时,S的值最大,最大值为280,
∴当日销售单价定为9元时,才能获得最大日销售利润是280元.
所以函数关系式为:y=
| 420 |
| x |
(2)根据题意可得:
S=(x-3)×
| 420 |
| x |
| 1260 |
| x |
(3)由题意可知:x≤3+3×200%,
∴3≤x≤9,
∵k=-1260<0,
∴S随x的增大而增大,
∴当x=9时,S的值最大,最大值为280,
∴当日销售单价定为9元时,才能获得最大日销售利润是280元.
点评:此题主要考查了反比例函数的应用,利用函数增减性得出是解题关键.

练习册系列答案
相关题目
 小明玩数学游戏,利用四张完全相同的小长方形纸板测量一张正方形纸板的边长,将它们如图放置,测量的数据如图,则这张正方形纸板的边长为( )
小明玩数学游戏,利用四张完全相同的小长方形纸板测量一张正方形纸板的边长,将它们如图放置,测量的数据如图,则这张正方形纸板的边长为( )| A、60cm | B、70cm |
| C、80cm | D、90cm |
 如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )| A、3cm | B、6cm |
| C、11cm | D、14cm |
关于函数y=x2-2x-3的叙述:
①当x>1时,y的值随x的增大而增大
②y的最小值是-3
③函数图象与x轴交点的横坐标是方程x2-2x-3=0的根
④函数图象与y轴交点的坐标是(0,-3)
⑤函数图象经过第一、二、三、四象限
其中正确的有( )
①当x>1时,y的值随x的增大而增大
②y的最小值是-3
③函数图象与x轴交点的横坐标是方程x2-2x-3=0的根
④函数图象与y轴交点的坐标是(0,-3)
⑤函数图象经过第一、二、三、四象限
其中正确的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
下列说法错误的是( )


| A、图①中直线l经过点A |
| B、图②中直线a,b相交于点A |
| C、图③中点C在线段AB上 |
| D、图④中射线CD与AB有公共点 |
 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.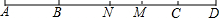 如图,AC=BD,BC:AD=5:9,M是BD的中点.
如图,AC=BD,BC:AD=5:9,M是BD的中点. 如图所示,点B,C是线段AD上任意两点,点M是AB的中点,点N是CD的中点.若AD=27,BC=5,则线段MN的长是
如图所示,点B,C是线段AD上任意两点,点M是AB的中点,点N是CD的中点.若AD=27,BC=5,则线段MN的长是