题目内容
关于函数y=x2-2x-3的叙述:
①当x>1时,y的值随x的增大而增大
②y的最小值是-3
③函数图象与x轴交点的横坐标是方程x2-2x-3=0的根
④函数图象与y轴交点的坐标是(0,-3)
⑤函数图象经过第一、二、三、四象限
其中正确的有( )
①当x>1时,y的值随x的增大而增大
②y的最小值是-3
③函数图象与x轴交点的横坐标是方程x2-2x-3=0的根
④函数图象与y轴交点的坐标是(0,-3)
⑤函数图象经过第一、二、三、四象限
其中正确的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
考点:二次函数的性质
专题:
分析:先把解析式配成顶点式,则可对①②进行判断;根据抛物线与x轴的交点问题对③进行判断;利用自变量为0时函数值为-3对④进行判断;根据二次函数图象与系数的关系对⑤进行判断.
解答:解:y=(x-1)2-4,则x>1时,y的值随x的增大而增大,所以①正确;
当x=1时,函数有最小值-4,所以②错误;
方程x2-2x-3=0的根可理解为函数值为0时所对应的自变量的值,所以函数图象与x轴交点的横坐标是方程x2-2x-3=0的根,所以③正确;
当x=0时,y=x2-2x-3=-3,所以函数图象与y轴交点的坐标是(0,-3),所以④正确;
图象的顶点在第四象限,开口向上,且与y轴的交点在x轴下方,所以函数图象经过第一、二、三、四象限,所以⑤正确.
故选C.
当x=1时,函数有最小值-4,所以②错误;
方程x2-2x-3=0的根可理解为函数值为0时所对应的自变量的值,所以函数图象与x轴交点的横坐标是方程x2-2x-3=0的根,所以③正确;
当x=0时,y=x2-2x-3=-3,所以函数图象与y轴交点的坐标是(0,-3),所以④正确;
图象的顶点在第四象限,开口向上,且与y轴的交点在x轴下方,所以函数图象经过第一、二、三、四象限,所以⑤正确.
故选C.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-b2a时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则r的取值范围是( )
| A、r<5 | B、r=5 |
| C、r>5 | D、r≥5 |
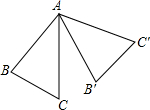 如图,将△ABC绕着顶点A逆时针旋转了70°后,得到△AB′C′,若∠B+∠C=130°,则∠CAB′的度数为( )
如图,将△ABC绕着顶点A逆时针旋转了70°后,得到△AB′C′,若∠B+∠C=130°,则∠CAB′的度数为( )| A、20° | B、50° |
| C、60° | D、70° |
 (1)已知线段AB长为6cm,点C是线段AB上一点,满足AC=
(1)已知线段AB长为6cm,点C是线段AB上一点,满足AC= 如图,B、C两点把线段AD分成2,4,3三部分,点P是AD的中点,已知CD=5,求线段PC的长.
如图,B、C两点把线段AD分成2,4,3三部分,点P是AD的中点,已知CD=5,求线段PC的长. 如图,下面表述正确的是
如图,下面表述正确的是