题目内容
8.已知等腰三角形的周长为12cm,若底边长为ycm,一腰长为xcm.则y与x的函数关系式是y=-2x+12;自变量x的取值范围是3<x<6.分析 根据三角形的周长公式可得:底边长=周长-2×腰长;再根据三角形三边关系定理:三角形任意两边之和大于第三边可得$\left\{\begin{array}{l}{2x>y}\\{x+y>x}\end{array}\right.$,再把y=12-2x代入可得$\left\{\begin{array}{l}{2x>12-2x}\\{12-2x>0}\end{array}\right.$,再解不等式组即可.
解答 解:依题意有:y=12-2x,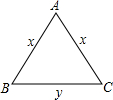
故y与x的函数关系式为:y=12-2x;
∵$\left\{\begin{array}{l}{2x>y}\\{x+y>x}\end{array}\right.$,
∴$\left\{\begin{array}{l}{2x>12-2x}\\{12-2x>0}\end{array}\right.$,
解得:3<x<6.
故自变量x的取值范围为3<x<6.
故答案为:y=12-2x;3<x<6.
点评 此题主要考查了列函数关系式,此题的难点是求自变量x的取值范围,关键是掌握三角形任意两边之和大于第三边.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
3. 如图,点A表示的实数是( )
如图,点A表示的实数是( )
 如图,点A表示的实数是( )
如图,点A表示的实数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | -$\sqrt{3}$ | D. | -$\sqrt{5}$ |
13.若|x-2|=2-x,则x的取值范围是( )
| A. | x<2 | B. | x≤2 | C. | x>2 | D. | x≥2 |
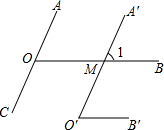 如图所示,OA∥O′A′,OB∥O′B′.
如图所示,OA∥O′A′,OB∥O′B′.