题目内容
14.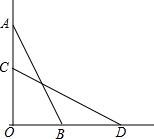 如图,梯子斜靠在与地面垂直的墙上,梯子AB与地面成60°角,当梯子的底端B向右滑1m到D时,梯子CD与地面成30°角,求梯子的长.
如图,梯子斜靠在与地面垂直的墙上,梯子AB与地面成60°角,当梯子的底端B向右滑1m到D时,梯子CD与地面成30°角,求梯子的长.
分析 设梯子的长为xm,根据特殊角的三角函数值表示出OC、OD,根据勾股定理列出方程,解方程即可.
解答 解:设梯子的长为xm,
∵∠ABO=60°,
∴OB=$\frac{1}{2}$x,
∵∠ODC=30°,
∴OC=$\frac{1}{2}$x,
在△OCD中,OC2+OD2=CD2,
即($\frac{1}{2}$x)2+($\frac{1}{2}$x+1)2=x2,
解得,x=1+$\sqrt{3}$,
答:梯子的长为(1+$\sqrt{3}$)m.
点评 本题考查的是勾股定理的应用,掌握勾股定理、正确运用数形结合思想是解题的关键.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
4.下列说法不正确的是( )
| A. | $\frac{1}{25}$的平方根是$±\frac{1}{5}$ | B. | $\root{3}{-27}$=-3 | ||
| C. | (-0.1)2的平方根是±0.1 | D. | $\sqrt{81}$的平方根±9 |
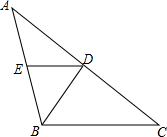 如图,在△ABC中,AB=BC,BD是∠ABC的平分线,DE∥BC.
如图,在△ABC中,AB=BC,BD是∠ABC的平分线,DE∥BC. 如图,四边形DEFG是△ABC的内接正方形,AB=BC=6cm,∠B=45°,则正方形DEFG的面积为多少?
如图,四边形DEFG是△ABC的内接正方形,AB=BC=6cm,∠B=45°,则正方形DEFG的面积为多少? 如图,△ABC中,∠B=30°,∠C=45°,AB=2$\sqrt{3}$,点E在边AB上,点D在边BC上,且满足∠AED=∠C,连接AD,若∠ADE=∠BAC.给出下列结论:①AD=BD;②AE=CD;③△BDE∽△ADB;④$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{3}$.其中正确的结论有①②④(把所有正确结论序号都填在横线上)
如图,△ABC中,∠B=30°,∠C=45°,AB=2$\sqrt{3}$,点E在边AB上,点D在边BC上,且满足∠AED=∠C,连接AD,若∠ADE=∠BAC.给出下列结论:①AD=BD;②AE=CD;③△BDE∽△ADB;④$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{3}$.其中正确的结论有①②④(把所有正确结论序号都填在横线上)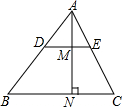 如图,△ABC,DE∥BC交AB、AC于D、E,AN⊥BC交DE于M点,若AD:DB=2:3,AM=3,则AN=$\frac{15}{2}$.若BC=8,则S△ADE=$\frac{24}{5}$.
如图,△ABC,DE∥BC交AB、AC于D、E,AN⊥BC交DE于M点,若AD:DB=2:3,AM=3,则AN=$\frac{15}{2}$.若BC=8,则S△ADE=$\frac{24}{5}$. 作图题:已知线段a,b(a<b,如图),求作矩形ABCD,使其一边长为a,另一边长为b.(保留作图痕迹,不写作法和证明过程)
作图题:已知线段a,b(a<b,如图),求作矩形ABCD,使其一边长为a,另一边长为b.(保留作图痕迹,不写作法和证明过程) 如图,已知AB⊥CD,AB∥EF,∠F=100°,求∠1的度数.
如图,已知AB⊥CD,AB∥EF,∠F=100°,求∠1的度数.