Question

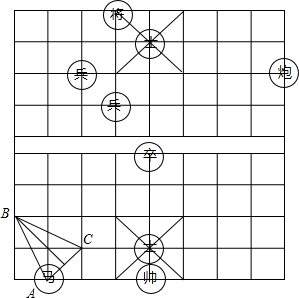亲爱的同学，你会玩中国象棋吗？如图所示的一盘象棋中．马走的两步棋从A到B再到C，若小正方形边长为1，求B到AC的距离．

Answer 1

考点：勾股定理的应用

专题：

分析：首先根据勾股定理可求出三角形ABC中AC边的边长，三角形ABC的面积等于正方形的面积减去三个直角三角形的面积，设AC边上的高为h，三角形ABC的面积还等于

1

2

AC×h，使两个面积值相等即可求出h的值．

解答：解：由于每个小正方形的边长为1，
则根据勾股定理可求：AC=

12+12

=

2

，
△ABC的面积为：4-

1

2

×1×2-

1

2

×1×2-

1

2

×1×1=1.5．
设AC边上的高为h，
则△ABC的面积为：

1

2

×AC×h=

2

2

h=1.5，
解得h=

3 2

2

．
故B到AC的距离是

3 2

2

．

点评：本题考查了勾股定理的应用和三角形的面积．首先根据勾股定理可求出三角形ABC中AC边的长度，然后利用正方形的面积减去三个直角三角形的面积可求出ABC的面积，三角形的面积等于

1

2

倍边长乘以这个边上的高，令两面积相等即可求出h的值．