题目内容
2.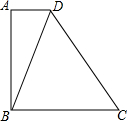 如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;
如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;(1)画出△CBD的高CE;
(2)请写出图中的一对全等三角形(不添加任何字母),并说明理由;
(3)若AD=2,CB=5,求DE的长.
分析 (1)过点C作出BD的垂线段CE即可;
(2)由AAS可以证明△ABD≌△ECB;
(3)由△ABD≌△ECB,得出BE=AD=2,BD=BC=5,再根据DE=BD-BE即可求解.
解答 解:(1)如图所示: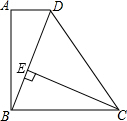
(2)△ABD≌△ECB,理由是:
∵AD∥BC,
∴∠ADB=∠EBC.
∵CE⊥BD,
∴∠CEB=90°,
∵∠A=90°,
∴∠CEB=∠A.
在△ABD与△ECB中,
$\left\{\begin{array}{l}{∠A=∠CEB}\\{∠ADB=∠EBC}\\{BD=CB}\end{array}\right.$,
∴△ABD≌△ECB;
(3)∵△ABD≌△ECB,
∴BE=AD=2,BD=BC=5,
∴DE=BD-BE=5-2=3.
点评 本题主要考查了全等三角形的判定与性质,三角形的高,熟练掌握全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
13.若a>b,则下列结论正确的是( )
| A. | a+2<b+2 | B. | a-5<b-5 | C. | $\frac{a}{3}$<$\frac{b}{3}$ | D. | 3a>3b |
10.若a<b,则下列结论中,不成立的是( )
| A. | a+3<b+3 | B. | a-2>b-2 | C. | $\frac{1}{2}$a<$\frac{1}{2}$b | D. | -2a>-2b |
17.已知x<y,则下列四个不等式中,不正确的是( )
| A. | -2x<-2y | B. | x-2<y-2 | C. | 2x<2y | D. | x+2<y+2 |
14. 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=25°,那么∠2的度数是( )
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=25°,那么∠2的度数是( )
 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=25°,那么∠2的度数是( )
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=25°,那么∠2的度数是( )| A. | 35° | B. | 30° | C. | 25° | D. | 20° |
12.下列不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}2x+9y=0\\ x+y=0\end{array}\right.$ | B. | 3x=4y=1 | C. | $\left\{\begin{array}{l}\frac{1}{x}-2y=2\\ x=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ |
 如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则菱形EGFH面积的最大值为20.
如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则菱形EGFH面积的最大值为20.


