题目内容
10.若a<b,则下列结论中,不成立的是( )| A. | a+3<b+3 | B. | a-2>b-2 | C. | $\frac{1}{2}$a<$\frac{1}{2}$b | D. | -2a>-2b |
分析 根据不等式的性质逐一判断,判断出结论不成立的是哪个即可.
解答 解:∵a<b,
∴a+3<b+3,
∴选项A成立;
∵a<b,
∴a-2<b-2,
∴选项B不成立;
∵a<b,
∴$\frac{1}{2}$a<$\frac{1}{2}$b,
∴选项C成立;
∵a<b,
∴-2a>-2b,
∴选项D成立.
故选:B.
点评 此题主要考查了不等式的性质,要熟练掌握,特别要注意在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.

练习册系列答案
相关题目
1.21300000用科学记数法表示是( )
| A. | 21.3×106 | B. | 2.13×105 | C. | 2.13×107 | D. | 21.3×105 |
18. 如图,点D、E、F分别是△ABC各边中点.DE等于4,则AC等于( )
如图,点D、E、F分别是△ABC各边中点.DE等于4,则AC等于( )
 如图,点D、E、F分别是△ABC各边中点.DE等于4,则AC等于( )
如图,点D、E、F分别是△ABC各边中点.DE等于4,则AC等于( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
15.若a>b>0,则下列结论正确的是( )
| A. | a-2<b-2 | B. | -2a>-2b | C. | $\frac{1}{2}$a<$\frac{1}{2}$b | D. | $\sqrt{a}$>$\sqrt{b}$ |
2.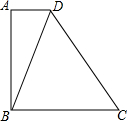 如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;
如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;
(1)画出△CBD的高CE;
(2)请写出图中的一对全等三角形(不添加任何字母),并说明理由;
(3)若AD=2,CB=5,求DE的长.
 如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;
如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;(1)画出△CBD的高CE;
(2)请写出图中的一对全等三角形(不添加任何字母),并说明理由;
(3)若AD=2,CB=5,求DE的长.
19.k、m、n为三个整数,若$\sqrt{90}$=k$\sqrt{10}$,$\sqrt{800}$=20$\sqrt{m}$,$\sqrt{180}$=6$\sqrt{n}$,则下列有关k、m、n的大小关系中,正确的是( )
| A. | m<k<n | B. | m=n<k | C. | m<n<k | D. | k<m=n |
20.已知点(-1,y1)、(3,y2)都在直线y=-2x+1上,则y1、y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |