题目内容
7. 如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则菱形EGFH面积的最大值为20.
如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则菱形EGFH面积的最大值为20.
分析 首先连接EF交AC于O,由四边形EGFH是菱形,易证得△CFO≌△AOE,可得AO=CO,继而求得AO的长,易证得△AOE∽△ABC,然后由相似三角形的对应边成比例,求得OE的长,再由当GH=AC时,菱形EGFH面积的最大,即可求得答案.
解答  解;连接EF交AC于O,
解;连接EF交AC于O,
∵四边形EGFH是菱形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中,
$\left\{\begin{array}{l}{∠FCO=∠OAB}\\{∠FOC=∠AOE}\\{OF=OE}\end{array}\right.$,
∴△CFO≌△AOE,
∴AO=CO,
∵AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=4$\sqrt{5}$,
∴AO=$\frac{1}{2}$AC=2$\sqrt{5}$,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴$\frac{AO}{AB}$=$\frac{OE}{BC}$,
∴$\frac{2\sqrt{5}}{8}$=$\frac{OE}{4}$,
∴OE=$\sqrt{5}$,
∴EF=2OE=2$\sqrt{5}$,
当GH=AC时,菱形EGFH面积的最大,最大值为:$\frac{1}{2}$AC•EF=$\frac{1}{2}$×4$\sqrt{5}$×2$\sqrt{5}$=20.
故答案为:20.
点评 此题考查了菱形的性质、矩形的性质、相似三角形的判定与性质以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 如图,点D、E、F分别是△ABC各边中点.DE等于4,则AC等于( )
如图,点D、E、F分别是△ABC各边中点.DE等于4,则AC等于( )
 如图,点D、E、F分别是△ABC各边中点.DE等于4,则AC等于( )
如图,点D、E、F分别是△ABC各边中点.DE等于4,则AC等于( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
15.若a>b>0,则下列结论正确的是( )
| A. | a-2<b-2 | B. | -2a>-2b | C. | $\frac{1}{2}$a<$\frac{1}{2}$b | D. | $\sqrt{a}$>$\sqrt{b}$ |
2.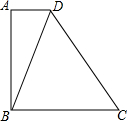 如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;
如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;
(1)画出△CBD的高CE;
(2)请写出图中的一对全等三角形(不添加任何字母),并说明理由;
(3)若AD=2,CB=5,求DE的长.
 如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;
如图,在四边形ABCD中,AD∥BC,BD=BC,∠A=90°;(1)画出△CBD的高CE;
(2)请写出图中的一对全等三角形(不添加任何字母),并说明理由;
(3)若AD=2,CB=5,求DE的长.
12.下列定理中,没有逆定理的是( )
| A. | 直角三角形两锐角互余 | |
| B. | 直角三角形两直角边的平方和等于斜边的平方 | |
| C. | 两直线平行,同位角相等 | |
| D. | 对顶角相等 |
19.k、m、n为三个整数,若$\sqrt{90}$=k$\sqrt{10}$,$\sqrt{800}$=20$\sqrt{m}$,$\sqrt{180}$=6$\sqrt{n}$,则下列有关k、m、n的大小关系中,正确的是( )
| A. | m<k<n | B. | m=n<k | C. | m<n<k | D. | k<m=n |
17.在实数$\frac{33}{7}$,-$\sqrt{2}$,0.1,0,2π,$\sqrt{9}$中,无理数的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 如图,△ABC中,AB=AC,AD是∠BAC的平分线,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
如图,△ABC中,AB=AC,AD是∠BAC的平分线,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )