题目内容
12. 如图,在?ABCD中,过对角线的交点O作两条直线分别与AB,BC,CD,DA交于点G,F,H,E.求证:四边形GFHE是平行四边形.
如图,在?ABCD中,过对角线的交点O作两条直线分别与AB,BC,CD,DA交于点G,F,H,E.求证:四边形GFHE是平行四边形.
分析 首先根据平行四边形的性质可得AO=CO,BO=DO,AD∥BC,再证明△AEO≌△CFO,进而得到EO=FO,进而得出GO=HO,可根据对角线互相平分的四边形是平行四边形进行判定.
解答 ∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD∥BC,
∴∠EAO=∠FCO,
在△AEO和△CFO中$\left\{\begin{array}{l}{AO=CO}\\{∠EAO=∠FCO}\\{∠AOE=COF}\end{array}\right.$
∴△AEO≌△CFO(AAS),
∴EO=FO,
同理可得:△BGO≌△DHO,
∴GO=HO,
∴四边形EGFH是平行四边形.
点评 此题主要考查了平行四边形的性质与判定,关键是掌握平行四边形对角线互相平分,对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目
3.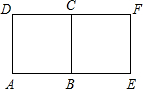 如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.
如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.
 如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.
如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.点A为数轴上表示-4的动点,当点A沿数轴移动4个单位长到B时,点B所表示的实数是( )
| A. | 0 | B. | -8或0 | C. | 0 | D. | 不同于以上答案 |
1. 如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
 如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
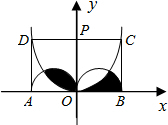 如图,矩形ABCD的长AB=4cm,点O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.以AB、OP所在直线为两轴建立直角坐标系,抛物线y=ax2经过C、D两点,则图中阴影部分的面积是$\frac{π}{2}$cm2.
如图,矩形ABCD的长AB=4cm,点O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.以AB、OP所在直线为两轴建立直角坐标系,抛物线y=ax2经过C、D两点,则图中阴影部分的面积是$\frac{π}{2}$cm2.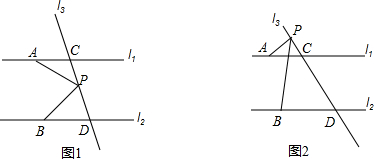
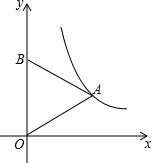 如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1).
如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1).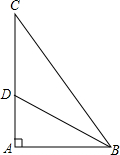 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=15,BD=17,则点D到BC的距离是8.
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=15,BD=17,则点D到BC的距离是8.