题目内容
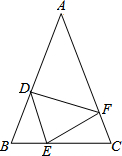 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.
考点:等腰三角形的判定与性质
专题:
分析:(1)根据等边对等角可得∠B=∠C,利用“边角边”证明△BDE和△CEF全等,根据全等三角形对应边相等可得DE=EF,再根据等腰三角形的定义证明即可;
(2)根据全等三角形对应角相等可得∠BDE=∠CEF,然后求出∠BED+∠CED=∠BED+∠BDE,再利用三角形的内角和定理和平角的定义求出∠B=∠DEF.
(2)根据全等三角形对应角相等可得∠BDE=∠CEF,然后求出∠BED+∠CED=∠BED+∠BDE,再利用三角形的内角和定理和平角的定义求出∠B=∠DEF.
解答:(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠BED+∠CED=∠BED+∠BDE,
∵∠B+(∠BED+∠BDE)=180°,
∠DEF+(∠BED+∠BDE)=180°,
∴∠B=∠DEF,
∵∠A=50°,AB=AC,
∴∠B=
(180°-50°)=65°,
∴∠DEF=65°.
∴∠B=∠C,
在△BDE和△CEF中,
|
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠BED+∠CED=∠BED+∠BDE,
∵∠B+(∠BED+∠BDE)=180°,
∠DEF+(∠BED+∠BDE)=180°,
∴∠B=∠DEF,
∵∠A=50°,AB=AC,
∴∠B=
| 1 |
| 2 |
∴∠DEF=65°.
点评:本题考查了等腰三角形的判定与性质,三角形的内角和定理,全等三角形的判定与性质,熟记各性质并确定出全等三角形是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )| A、40° | B、45° |
| C、50° | D、55° |
 已知:如图,DE∥BC,AD:DB=1:2,则下列结论不正确的是( )
已知:如图,DE∥BC,AD:DB=1:2,则下列结论不正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,有点A、B、C、D,请画出一点P,使PA=PB,PC=PD.
如图,有点A、B、C、D,请画出一点P,使PA=PB,PC=PD. 如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在
如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在 如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为 已知:如图,在⊙O中,∠AOD=∠BOC.求证:弧AB与弧CD是等弧.
已知:如图,在⊙O中,∠AOD=∠BOC.求证:弧AB与弧CD是等弧.