题目内容
 已知:如图,在⊙O中,∠AOD=∠BOC.求证:弧AB与弧CD是等弧.
已知:如图,在⊙O中,∠AOD=∠BOC.求证:弧AB与弧CD是等弧.考点:圆心角、弧、弦的关系
专题:证明题
分析:根据圆心角、弧、弦的关系只要证明∠AOB=∠COD即可.
解答:证明:∵∠AOD=∠BOC,
∴∠AOD-∠AOC=∠BOC-∠AOC,即∠AOB=∠COD,
∴弧AB与弧CD是等弧.
∴∠AOD-∠AOC=∠BOC-∠AOC,即∠AOB=∠COD,
∴弧AB与弧CD是等弧.
点评:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点D是AB边的中点,以点C为圆心,2.4cm为半径作圆,则点D与⊙C的位置关系是( )
| A、点D在⊙C上 |
| B、点D在⊙C外 |
| C、点D在⊙C内 |
| D、不能确定 |
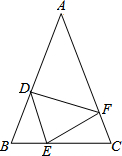 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE. 如图,PM=PN,PM垂直OA,PN垂直OB,∠BOC=30°,则∠AOB=
如图,PM=PN,PM垂直OA,PN垂直OB,∠BOC=30°,则∠AOB=