题目内容
7.如果实数x、y满足方程组$\left\{\begin{array}{l}{x+3y=0}\\{2x+3y=3}\end{array}\right.$,求代数式($\frac{xy}{x+y}$+2)÷$\frac{1}{x+y}$.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,求出方程组的解得到x与y的值,代入计算即可求出值.
解答 解:原式=$\frac{xy}{x+y}$•(x+y)+2•(x+y)=xy+2x+2y,
方程组$\left\{\begin{array}{l}{x+3y=0}\\{2x+3y=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$,
当x=3,y=-1时,原式=-3+6-2=1.
点评 此题考查了分式的化简求值,解二元一次方程组,掌握分式的化简方法与解方程组的方法是解决问题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
18.下列各组图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 平行四边形、菱形、正方形 | B. | 等边三角形、矩形、正方形 | ||
| C. | 菱形、正方形、矩形 | D. | 等边三角形、矩形、圆 |
15.下列等式中,是一元一次方程的个数有( )
①5+4x=11;②3x-2x=1;③2x+y=5;④x2-5x+6=0.
①5+4x=11;②3x-2x=1;③2x+y=5;④x2-5x+6=0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

 如图,EF与AB、CD分别相交于M、N,EF⊥CD,∠1=63°,∠2=27°,试说明AB∥CD.
如图,EF与AB、CD分别相交于M、N,EF⊥CD,∠1=63°,∠2=27°,试说明AB∥CD.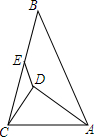 如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E为BC中点,则DE的长1.5cm.
如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E为BC中点,则DE的长1.5cm.