题目内容
11.在⊙O中,AB为直径,C为⊙O上一点.
(1)如图1,过点C作⊙O的切线,与AB延长线相交于点P,若∠CAB=27°,求∠P的度数;
(2)如图2,D为弧AB上一点,OD⊥AC,垂足为E,连接DE并延长,与AB的延长线交于点P,若∠CAB=10°,求∠P的大小.
分析 (1)连接OC,首先根据切线的性质得到∠OCP=90°,利用∠CAB=27°得到∠COB=2∠CAB=54°,然后利用直角三角形两锐角互余即可求得答案;
(2)根据OD⊥AC,从而求得∠AOE=90°-∠EAO=80°,然后利用圆周角定理求得∠ACD=$\frac{1}{2}$∠AOD=40°,最后利用三角形的外角的性质求解即可.
解答 解:(1)如图①,连接OC,
∵⊙O与PC相切于点C,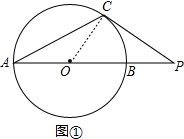
∴OC⊥PC,即∠OCP=90°,
∵∠CAB=27°,
∴∠COB=2∠CAB=54°,
在Rt△AOE中,∠P+∠COP=90°,
∴∠P=90°-∠COP=36°;
(2)∵OD⊥AC,即∠AEO=90°,
在Rt△AOE中,由∠EAO=10°,
得∠AOE=90°-∠EAO=80°,
∴∠ACD=$\frac{1}{2}$∠AOD=40°,
∵∠ACD是△ACP的一个外角,
∴∠P=∠ACD-∠A=40°-10°=30°.
点评 本题考查了切线的性质,解题的关键是能够利用圆的切线垂直于经过切点的半径得到直角三角形.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
3.关于x的方程(a-5)x2-4x-1=0有实数根,则a满足( )
| A. | a≥1 | B. | a>1且 a≠5 | C. | a≥1且 a≠5 | D. | a≠5 |

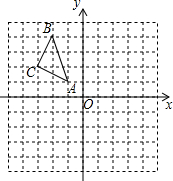 如图,A(-1,1),B(-2,4),C(-3,2).
如图,A(-1,1),B(-2,4),C(-3,2).