题目内容
9.在△ABC中,设$\overrightarrow{CA}=\overrightarrow a$,$\overrightarrow{CB}=\overrightarrow b$,P是中线AE与中线CF的交点,则$\overrightarrow{BP}$=$\frac{1}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$.(用$\overrightarrow a,\overrightarrow b$表示)分析 首先根据题意画出图形,利用三角形法则,求得$\overrightarrow{EA}$,又由P是中线AE与中线CF的交点,利用重心的性质,即可求得$\overrightarrow{EP}$,继而求得答案.
解答  解:∵$\overrightarrow{CB}=\overrightarrow b$,AE是△ABC的中线,
解:∵$\overrightarrow{CB}=\overrightarrow b$,AE是△ABC的中线,
∴$\overrightarrow{EC}$=$\overrightarrow{BE}$=-$\frac{1}{2}$$\overrightarrow{CB}$=-$\frac{1}{2}$$\overrightarrow{b}$,
∵$\overrightarrow{CA}=\overrightarrow a$,
∴$\overrightarrow{EA}$=$\overrightarrow{EC}$+$\overrightarrow{CA}$=-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{a}$,
∵P是中线AE与中线CF的交点,
∴$\overrightarrow{EP}$=$\frac{1}{3}$$\overrightarrow{EA}$=$\frac{1}{3}$(-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{a}$)=$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{6}$$\overrightarrow{b}$,
∴$\overrightarrow{BP}$=$\overrightarrow{BE}$+$\overrightarrow{EP}$=-$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{6}$$\overrightarrow{b}$=$\frac{1}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$.
故答案为:$\frac{1}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$.
点评 此题考查了平面向量的知识以及三角形重心的性质.注意掌握三角形法则的应用是解此题的关键.

| A. | 5或3 | B. | 3 | C. | 1 | D. | 1或3或5 |
| A. | 9或-9 | B. | 9或-1 | C. | 1或-1 | D. | -9或-1 |
| A. | 0 | B. | 0和1 | C. | 只有正数 | D. | 0和正数 |
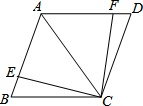 (1)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.
(1)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.
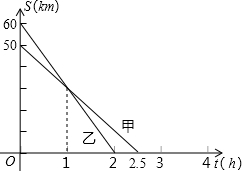 已知A、B、C三地在同一条笔直的公路上,甲、乙两人骑自行车分别从B、C两地前往A地.他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
已知A、B、C三地在同一条笔直的公路上,甲、乙两人骑自行车分别从B、C两地前往A地.他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题: 如图,已知数轴上点A表示的数为6,B是你数轴上一点,且AB=10,动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为6,B是你数轴上一点,且AB=10,动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.