题目内容
19.如图,图1中共有5个三角形,在图2中共有9个三角形,在图3中共有13个三角形 …在第8个图形中共有33个三角形.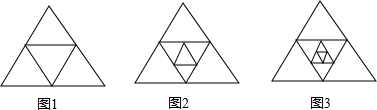
分析 由题意可知:图1中共有4+1=5个三角形,图2中共有4+4+1=9个三角形,在图3中共有4+4+4+1=13个三角形 …由此得出第n个图形中有4n+1个三角形,由此求得在第8个图形中共有8×4+1=33个三角形.
解答 解:∵图1中共有4+1=5个三角形,
在图2中共有4+4+1=9个三角形,
在图3中共有4+4+4+1=13个三角形,
…
∴第n个图形中有4n+1个三角形9,
∴在第8个图形中共有8×4+1=33个三角形.
故答案为:9,13,33.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
14.⊙O的半径为4cm,若点P到圆心的距离为3cm,点P在( )
| A. | 圆内 | B. | 圆上 | C. | 圆外 | D. | 无法确定 |
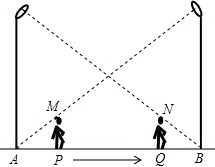 如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
 如图所示,∠A=∠D=90°,点O是BC的中点,问A,B,C,D四个点是否都在以O为圆的同一个圆上.
如图所示,∠A=∠D=90°,点O是BC的中点,问A,B,C,D四个点是否都在以O为圆的同一个圆上.