题目内容
17.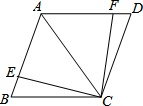 (1)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.
(1)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.(2)某花圃用花盆培育某种花苗,经过实验发现每盆的盈利于每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆没增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
分析 (1)根据菱形对角线的性质,可知一条对角线平分一组对角,即∠FAC=∠EAC,再根据边角边即可证明△ACE≌△ACF.
(2)根据已知假设每盆花苗增加x株,则每盆花苗有(x+3)株,得出平均单株盈利为(3-0.5x)元,由题意得(x+3)(3-0.5x)=10求出即可.
解答 解:(1)证明:∵AC是菱形ABCD的对角线,
∴∠FAC=∠EAC,
在△ACE和△ACF中,
$\left\{\begin{array}{l}{AE=AF}\\{∠EAC=∠FAC}\\{AC=AC}\end{array}\right.$,
∴△ACE≌△ACF(SAS).
(2)设每盆花苗增加x株,则每盆花苗有(x+3)株,
平均单株盈利为:(3-0.5x)元,
由题意得:(x+3)(3-0.5x)=10.
化简,整理,的x2-3x+2=0.
解这个方程,得x1=1,x2=2,
则3+1=4,
2+3=5.
答:每盆应植4株或者5株.
点评 此题考查了一元二次方程的应用及全等三角形的判定,根据每盆花苗株数×平均单株盈利=总盈利得出方程是解题关键.

练习册系列答案
相关题目
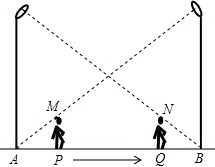 如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB. 如图所示,∠A=∠D=90°,点O是BC的中点,问A,B,C,D四个点是否都在以O为圆的同一个圆上.
如图所示,∠A=∠D=90°,点O是BC的中点,问A,B,C,D四个点是否都在以O为圆的同一个圆上.