题目内容
12.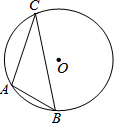 如图,已知⊙O的直径为8cm,A、B、C三点在⊙O上,且∠ACB=30°,则AB长4cm.
如图,已知⊙O的直径为8cm,A、B、C三点在⊙O上,且∠ACB=30°,则AB长4cm.
分析 作直径AD,连接BD,根据圆周角定理得到∠ABD=90°,∠D=∠ACB=30°,根据直角三角形的性质解答.
解答 解: 作直径AD,连接BD,
作直径AD,连接BD,
∴∠ABD=90°,
由圆周角定理得,∠D=∠ACB=30°,
∴AB=$\frac{1}{2}$AD=4cm,
故答案为:4cm.
点评 本题考查的是圆周角定理的应用,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半、直径所对的圆周角是直角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )
如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )
 如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )
如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )| A. | $\frac{4π}{3}$$-\sqrt{3}$ | B. | $\frac{4π}{3}$-2$\sqrt{3}$ | C. | $\frac{2π}{3}$$-\sqrt{3}$ | D. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ |
17.在平面直角坐标系中,点P(-1,2)向上平移3个单位长度后的坐标是( )
| A. | (2,2) | B. | (-4,2) | C. | (-1,5) | D. | (-1,-1) |
 海轮以每小时30nmile的速度航行,在点A处测得海上油井P在它的南偏东60°方向,向北航行40min后到达B处,测得油井P在南偏东30°方向,海轮改北偏东60在再航行120min到达C处,求P,C间的距离及此时点C在油井P的什么方向.
海轮以每小时30nmile的速度航行,在点A处测得海上油井P在它的南偏东60°方向,向北航行40min后到达B处,测得油井P在南偏东30°方向,海轮改北偏东60在再航行120min到达C处,求P,C间的距离及此时点C在油井P的什么方向.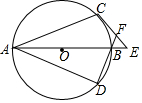 如图,AB为⊙O的直径,AC,AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为3,∠E=45°,则CF的长为6-3$\sqrt{2}$.
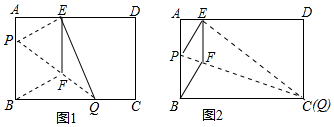
如图,AB为⊙O的直径,AC,AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为3,∠E=45°,则CF的长为6-3$\sqrt{2}$. 已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.
已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.