题目内容
15.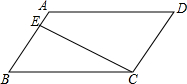 如图,在?ABCD中,AB∥CD,BC∥AD,CE⊥AB,垂足是E,AB=3,BC=4,∠B=60°,把四边形ABCD沿直线CE翻折,那么重叠部分的面积为$\frac{5\sqrt{3}}{3}$.
如图,在?ABCD中,AB∥CD,BC∥AD,CE⊥AB,垂足是E,AB=3,BC=4,∠B=60°,把四边形ABCD沿直线CE翻折,那么重叠部分的面积为$\frac{5\sqrt{3}}{3}$.
分析 将△BCE沿CE翻折得到△ECF,重叠部分就是四边形AECH.作HN⊥BF于N,根据S四边形AECH=S△ECF-S△AHF即可解决问题.
解答 解: 将△BCE沿CE翻折得到△ECF,重叠部分就是四边形AECH.作HN⊥BF于N.
将△BCE沿CE翻折得到△ECF,重叠部分就是四边形AECH.作HN⊥BF于N.
在RT△BCE中,∵∠BEC=90°,BC=4,∠B=60°,
∴∠BCE=30°,BE=$\frac{1}{2}$BC=2,EC=2$\sqrt{3}$,
∴BE=EF=2,AF=AE=1,
∵CD∥AF,
∴FH:HC=AF:CD=1:2
∵NH∥CE,
∴$\frac{NH}{EC}$=$\frac{FH}{FC}$=$\frac{1}{4}$,
∴NH=$\frac{\sqrt{3}}{2}$,
∴S四边形AECH=S△ECF-S△AHF=$\frac{1}{2}$$•2•2\sqrt{3}$-$\frac{1}{2}$•1•$\frac{\sqrt{3}}{2}$=$\frac{7\sqrt{3}}{4}$.
故答案为$\frac{7\sqrt{3}}{4}$.
点评 本题考查翻折变换、平行四边形性质,直角三角形30度角性质,勾股定理等知识,解题的关键是学会分割法求面积,属于中考常考题型.

练习册系列答案
相关题目
5.在平面直角坐标系xOy中,点M(a,1)在一次函数y=-x+3的图象上,则点N(2a-1,a)所在的象限是第( )
| A. | 一象限 | B. | 二象限 | C. | 四象限 | D. | 不能确定 |
3.已知关于x的不等式组$\left\{\begin{array}{l}{x>-2}\\{x>-1}\\{x<a}\end{array}\right.$无解,则a的取值范围是( )
| A. | a≤-1 | B. | a≥2 | C. | -1<a<2 | D. | a<-1或a>-2 |
20.“武夷水秀”以特有的光影效果,吸引众多市民前去观看.特别是五一当天,共演了7场,平均每场有1200人观看,这天观看的总人数用科学记数法可以表示为( )
| A. | 0.12×104 | B. | 1.2×103 | C. | 8.4×103 | D. | 84×102 |




 如图,⊙O的内接正六边形的边长是6,则边心距为3$\sqrt{3}$.
如图,⊙O的内接正六边形的边长是6,则边心距为3$\sqrt{3}$.