题目内容
17.如果a=(-2016)0,b=(-0.1)-2016,c=(-$\frac{6}{5}$)-2,那么用“<”将a,b,c的大小关系连接起来为:c<a<b.分析 先依据零指数幂的性质、负整数指数幂的性质计算,然后再比较a,b,c的大小即可.
解答 解:a=(-2016)0=1,b=(-0.1)-2016=(-10)2016=102016,c=(-$\frac{6}{5}$)-2=(-$\frac{5}{6}$)2=$\frac{25}{36}$.
∴c<a<b.
故答案为:c<a<b.
点评 本题主要考查的是负整数指数幂的性质、零指数幂的性质,熟练掌握相关性质是解题的关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
8.下列各式与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{8}$ | C. | $\sqrt{2}$ | D. | $\sqrt{12}$ |
6. 在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的限距点的定义如下:若P′为直线PC与⊙C的一个交点,满足r≤PP′≤2r,则称P′为点P关于⊙C的限距点,如图为点P及其关于⊙C的限距点P′的示意图.
在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的限距点的定义如下:若P′为直线PC与⊙C的一个交点,满足r≤PP′≤2r,则称P′为点P关于⊙C的限距点,如图为点P及其关于⊙C的限距点P′的示意图.
(1)当⊙O的半径为1时.
①分别判断点M(3,4),N($\frac{5}{2}$,0),T(1,$\sqrt{2}$)关于⊙O的限距点是否存在?若存在,求其坐标;
②点D的坐标为(2,0),DE,DF分别切⊙O于点E,点F,点P在△DEF的边上.若点P关于⊙O的限距点P′存在,求点P′的横坐标的取值范围;
(2)保持(1)中D,E,F三点不变,点P在△DEF的边上沿E→F→D→E的方向运动,⊙C的圆心C的坐标为(1,0),半径为r,请从下面两个问题中任选一个作答.
 在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的限距点的定义如下:若P′为直线PC与⊙C的一个交点,满足r≤PP′≤2r,则称P′为点P关于⊙C的限距点,如图为点P及其关于⊙C的限距点P′的示意图.
在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的限距点的定义如下:若P′为直线PC与⊙C的一个交点,满足r≤PP′≤2r,则称P′为点P关于⊙C的限距点,如图为点P及其关于⊙C的限距点P′的示意图.(1)当⊙O的半径为1时.
①分别判断点M(3,4),N($\frac{5}{2}$,0),T(1,$\sqrt{2}$)关于⊙O的限距点是否存在?若存在,求其坐标;
②点D的坐标为(2,0),DE,DF分别切⊙O于点E,点F,点P在△DEF的边上.若点P关于⊙O的限距点P′存在,求点P′的横坐标的取值范围;
(2)保持(1)中D,E,F三点不变,点P在△DEF的边上沿E→F→D→E的方向运动,⊙C的圆心C的坐标为(1,0),半径为r,请从下面两个问题中任选一个作答.
| 问题1 | 问题2 |
| 若点P关于⊙C的限距点P′存在,且P′随点P的运动所形成的路径长为πr,则r的最小值为 $\frac{\sqrt{3}}{9}$. | 若点P关于⊙C的限距点P′不存在,则r的取值范围为 0<r<$\frac{1}{6}$. |
7.某中学随机调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
则这50名学生这一周在校的平均体育锻炼时间的中位数是( )
| 时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 10 | 15 | 20 | 5 |
| A. | 6 | B. | 6.5 | C. | 7 | D. | 8 |
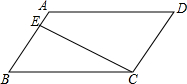 如图,在?ABCD中,AB∥CD,BC∥AD,CE⊥AB,垂足是E,AB=3,BC=4,∠B=60°,把四边形ABCD沿直线CE翻折,那么重叠部分的面积为$\frac{5\sqrt{3}}{3}$.
如图,在?ABCD中,AB∥CD,BC∥AD,CE⊥AB,垂足是E,AB=3,BC=4,∠B=60°,把四边形ABCD沿直线CE翻折,那么重叠部分的面积为$\frac{5\sqrt{3}}{3}$. 如图:我国渔政船310船在南海海面上沿正东方向匀速航行,在A点观测到我渔船C在北偏东方向的我国某传统渔场捕鱼作业.若渔政310船航向不变,航行半小时后到达B点,观测我渔船C在东北方向上.问:渔政310船再按原航向航行多长时间,渔船C离渔政310船的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
如图:我国渔政船310船在南海海面上沿正东方向匀速航行,在A点观测到我渔船C在北偏东方向的我国某传统渔场捕鱼作业.若渔政310船航向不变,航行半小时后到达B点,观测我渔船C在东北方向上.问:渔政310船再按原航向航行多长时间,渔船C离渔政310船的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值.) 如图,已知四边形ABDE为平行四边形,过E点作EC⊥DC交BD的延长线于点C,AE=DC,其中AB=15,则AC=15.
如图,已知四边形ABDE为平行四边形,过E点作EC⊥DC交BD的延长线于点C,AE=DC,其中AB=15,则AC=15.