��Ŀ����
13�������Ŀ�ͨΪ��������ij��д����˷��㣮�����ݵ��Ϸʣ�·��Ϊ360ǧ�ף�ij�˶�����ƽ���ٶȱ���ͨ�г���50%������ʱ�����ͨ�г���1Сʱ����ö�����ƽ���ٶȣ���1���ټ�ͬѧ����ͨ�г����ٶ�Ϊx���г��в������ķ��̣�$\frac{360}{x}=\frac{360}{1.5x}+$1
����ͬѧ�趯��������ʱ�� Ϊy���г��в������ķ��̣�$\frac{360}{y}$=$\frac{1.5��360}{����}$
��2����ѡ������һ��ͬѧ���跨��д�������Ľ����̣�
���� ����ͨ�г����ٶ�ΪΪxkm/h��������ƽ���ٶ�Ϊ1.5xkm/h�������߹���ͬ��·��360km�����������õ�ʱ�������ͨ�г����õ�ʱ����1Сʱ���з�����⣮
��� �⣺�ټ�ͬѧ����ͨ�г����ٶ�Ϊx���г��в������ķ��̣�$\frac{360}{x}=\frac{360}{1.5x}+$ 1
����ͬѧ�� ����������ʱ��Ϊy���г��в������ķ��̣�$\frac{360}{y}=\frac{1.5��360}{y+1}$
�ʴ�Ϊ����ͨ�г����ٶȣ�1������������ʱ�䣬y+1��
��2������ͨ�г����ٶ�ΪΪxkm/h��������ƽ���ٶ�Ϊ1.5xkm/h��
������ã�$\frac{360}{x}$-$\frac{360}{1.5x}$=1��
��ã�x=120��
�����飬x=120��ԭ��ʽ���̵Ľ⣬�ҷ������⣮
������ƽ���ٶ�=120��1.5=180km/h��
�𣺸��˶�����ƽ���ٶ�Ϊ180km/h��
���� ���⿼���˷�ʽ���̵�Ӧ�ã������Ĺؼ��Ƕ������⣬���δ֪�����ҳ����ʵĵ�����ϵ���з�����⣬ע����飮

��ϰ��ϵ�д�
�����Ŀ
1���ڵ�����ABC�У�AB=5cm��BC=7cm���������ABC���ܳ�Ϊ��������
| A�� | 12cm | B�� | 17cm | C�� | 19cm | D�� | 17cm��19cm |
18��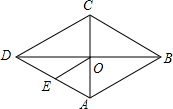 ��ͼ��������ABCD�У��Խ���AC��BD���ڵ�O��EΪAD���е㣬����ABCD���ܳ�Ϊ32����OE�ij����ڣ�������
��ͼ��������ABCD�У��Խ���AC��BD���ڵ�O��EΪAD���е㣬����ABCD���ܳ�Ϊ32����OE�ij����ڣ�������
 ��ͼ��������ABCD�У��Խ���AC��BD���ڵ�O��EΪAD���е㣬����ABCD���ܳ�Ϊ32����OE�ij����ڣ�������
��ͼ��������ABCD�У��Խ���AC��BD���ڵ�O��EΪAD���е㣬����ABCD���ܳ�Ϊ32����OE�ij����ڣ�������| A�� | 2 | B�� | 4 | C�� | 8 | D�� | 16 |
5��ijѧУ�ƻ���֯500�˲μ����ʵ�������ij������˾��Ǣ��֪�ù�˾��A��B�����ֿͳ������ǵ��ؿ�������������ʾ��
�����㣬����A��B�Ϳͳ���13����Ϊ������������A�Ϳͳ�x��������Ҫ��ش��������⣺
��1���ú�x�Ĵ���ʽ��д�±���
��2���������������������ʹ�ܵ��������ͣ����Ϊ���٣�
| A�Ϳͳ� | B�Ϳͳ� | |
| �ؿ�������/���� | 45 | 28 |
| ���Ԫ/���� | 400 | 250 |
��1���ú�x�Ĵ���ʽ��д�±���
| ������������ | �ؿ������ˣ� | ���Ԫ�� | |
| A�Ϳͳ� | x | 45x | 400x |
| B�Ϳͳ� | 13-x | 28��13-x�� | 250��13-x�� |
3��ֱ�������ε�һ��ֱ�DZ߳�Ϊ$\sqrt{2}$cm��б�߳�Ϊ$\sqrt{10}$cm����������ε����Ϊ��������
| A�� | 2 | B�� | 2$\sqrt{2}$ | C�� | 2$\sqrt{3}$ | D�� | 4 |
 ��ͼ����A��x���������ϵ�����һ�㣬����A��EF��y�ᣬ�ֱ���������y1=$\frac{{k}_{{\;}_{1}}}{x}$��y1��0����y2=$\frac{{k}_{2}}{x}$��y2��0����ͼ���ڵ�E��F����$\frac{EA}{FA}$=$\frac{5}{3}$������OE��OF�������н��ۣ���������������ͼ�����x��Գƣ��ڡ�EOF�����Ϊ$\frac{1}{2}$��k1-k2������$\frac{{k}_{1}}{{k}_{2}}$=-$\frac{3}{5}$���ܵ���EOF=90��ʱ��$\frac{OE}{OF}$=$\frac{\sqrt{15}}{3}$��������ȷ���ǣ�������
��ͼ����A��x���������ϵ�����һ�㣬����A��EF��y�ᣬ�ֱ���������y1=$\frac{{k}_{{\;}_{1}}}{x}$��y1��0����y2=$\frac{{k}_{2}}{x}$��y2��0����ͼ���ڵ�E��F����$\frac{EA}{FA}$=$\frac{5}{3}$������OE��OF�������н��ۣ���������������ͼ�����x��Գƣ��ڡ�EOF�����Ϊ$\frac{1}{2}$��k1-k2������$\frac{{k}_{1}}{{k}_{2}}$=-$\frac{3}{5}$���ܵ���EOF=90��ʱ��$\frac{OE}{OF}$=$\frac{\sqrt{15}}{3}$��������ȷ���ǣ������� ��ͼ����֪��E��F��ֱ��AB�ϣ���G���߶�CD�ϣ�ED��FG���ڵ�H����C=��EFG����CED=��GHD��
��ͼ����֪��E��F��ֱ��AB�ϣ���G���߶�CD�ϣ�ED��FG���ڵ�H����C=��EFG����CED=��GHD��