题目内容
10.观察:x2+2x+1=0的两根x1=x2=-1x2+3x+2=0的两根x1=-1 x2=-2
x2+4x+3=0的两根x1=-1 x2=-3
x2+5x+4=0的两根x1=-1 x2=-4
若方程x2+mx+n=0满足以上规律,则此方程的解为x1=-1,x2=-a.
分析 根据已知x2+2x+1=0的两根x1=x2=-1;x2+3x+2=0的两根x1=-1,x2=-2;x2+4x+3=0的两根x1=-1,x2=-3;x2+5x+4=0的两根x1=-1,x2=-4;可知满足以上规律的方程x2+mx+n=0的解.
解答 解:∵x2+2x+1=0的两根x1=x2=-1;
x2+3x+2=0的两根x1=-1,x2=-2;
x2+4x+3=0的两根x1=-1,x2=-3;
x2+5x+4=0的两根x1=-1,x2=-4;
∴方程x2+(a+1)x+a=0的解为x1=-1,x2=-a,
∴若方程x2+mx+n=0满足以上规律,则此方程的解为x1=-1,x2=-a.
故答案为x1=-1,x2=-a.
点评 本题考查了一元二次方程的解的意义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
18.下列因式分解正确的是( )
| A. | 12abc-9a2b2=3abc(4-3ab) | B. | 3m2n-3mn+6n=3n(m2-m+2) | ||
| C. | -x2+xy-xz=x(x+y-z) | D. | a2b+5ab-b=b(a2+5a) |
5.下列计算正确的是( )
| A. | 8x9÷4x3=2x3 | B. | k7+k7=2k14 | ||
| C. | a8•a8=2a16 | D. | 2ab2c÷(-$\frac{1}{2}$)ab2=-4c |
2.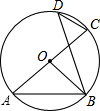 如图,AC是⊙O的直径,点B,D在⊙O上,那么图中等于∠BOC一半的角有( )
如图,AC是⊙O的直径,点B,D在⊙O上,那么图中等于∠BOC一半的角有( )
 如图,AC是⊙O的直径,点B,D在⊙O上,那么图中等于∠BOC一半的角有( )
如图,AC是⊙O的直径,点B,D在⊙O上,那么图中等于∠BOC一半的角有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | l个 |
