题目内容
阅读材料:
已知,如图(1),在面积为S的△ABC中,BC=a,AC=b,AB=c,内切圆O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
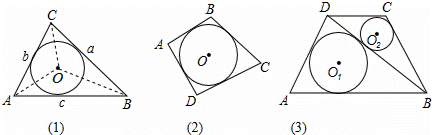
∵S=S△OBC+S△OAC+S△OAB=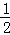 BC•r+
BC•r+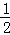 AC•r+
AC•r+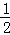 AB•r=
AB•r=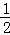 (a+b+c)r.
(a+b+c)r.
∴r=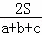 .
.
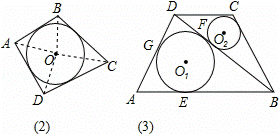
(1)类比推理:若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r;
(2)理解应用:如图(3),在四边形ABCD中,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,⊙O1与△ABD切点分别为E、F、G,设它们的半径分别为r1和r2,若∠ADB=90°,AE=4,BC+CD=10,S△DBC=9,r2=1,求r1的值.
解:(1)连接OA,OB,OC,OD,
∵S四边形ABCD=S△AOB+S△BOC+S△AOD+S△COD=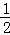 (a+b+c+d)r,
(a+b+c+d)r,
∴r=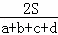 ;
;
(2)∵S△DBC=9,r2=1,
∴BC+CD+BD=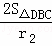 =18,
=18,
∵BC+CD=10,
∴BD=8.
∵⊙O1是△ABD的内切圆,
∴AE=AG=4,BE=BF,DF=DG,
∴DG+BE=BD=8,
∴设DG=x,则BE=8﹣x,
∵∠ADB=90°,
∴AD2+BD2=AB2,即(4+x)2+82=(4+8﹣x)2,解得x=2,
∴AD=AG+DG=4+2=6,
∴S△ABD=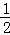 AD•BD=
AD•BD=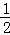 ×6×8=24,
×6×8=24,
∵AD+AB+BD=AG+AE+(DG+BE)+BD=4+4+8+8=24,
∴r1=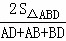 =
= =2.
=2.

练习册系列答案
相关题目

 .
.
 .
.
 .
.