题目内容
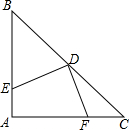 Rt△ABC中,AB=AC=2,∠A=90°,D为BC中点,点E,F分别在AB,AC上,且BE=AF,
Rt△ABC中,AB=AC=2,∠A=90°,D为BC中点,点E,F分别在AB,AC上,且BE=AF,(1)求证:ED=FD;
(2)求证:DF⊥DE;
(3)求四边形AFDE的面积.
考点:全等三角形的判定与性质
专题:
分析:(1)连接AD,可证△ADE≌△CDF,即可解题;
(2)由(1)可得∠EDA=∠FDC,可证∠EDF=90°即可解题;
(3)根据四边形AFDE的面积等于△ADC的面积即可解题.
(2)由(1)可得∠EDA=∠FDC,可证∠EDF=90°即可解题;
(3)根据四边形AFDE的面积等于△ADC的面积即可解题.
解答:(1)证明:连结AD,
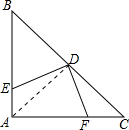
∵D为BC中点,
∴DA=DC,∠DAB=45°,
∵BE=AF,BA=AC,
∴AE=CF,
∵Rt△ABC中,AB=AC,
∴∠B=∠C=45°,
∴∠C=∠DAB,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴ED=FD;
(2)证明:由(1)可得∠EDA=∠FDC,
∵∠ADC=90°
∴∠EDF=90°,
∴DF⊥DE;
(3)解:∵△ADE≌△CDF,
∴SAFDE=S△ADC,
∵S△ADC=
S△ABC,
∴SAFDE=
S△ABC=2.

∵D为BC中点,
∴DA=DC,∠DAB=45°,
∵BE=AF,BA=AC,
∴AE=CF,
∵Rt△ABC中,AB=AC,
∴∠B=∠C=45°,
∴∠C=∠DAB,
在△ADE和△CDF中,
|
∴△ADE≌△CDF(SAS),
∴ED=FD;
(2)证明:由(1)可得∠EDA=∠FDC,
∵∠ADC=90°
∴∠EDF=90°,
∴DF⊥DE;
(3)解:∵△ADE≌△CDF,
∴SAFDE=S△ADC,
∵S△ADC=
| 1 |
| 2 |
∴SAFDE=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ADE≌△CDF是解题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,已知AB=AD,使用“A.A.S.”能判定△ABC≌△ADE的是( )
如图,已知AB=AD,使用“A.A.S.”能判定△ABC≌△ADE的是( )| A、∠B=∠C |
| B、AC=AD |
| C、BC=DE |
| D、∠ACB=∠AED |
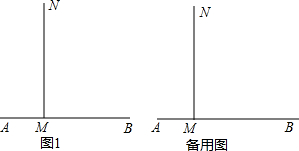 已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4.
已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4.