Question

【题目】如图，在正方形中，是边上的一动点（不与点，重合），连接，点关于直线的对称点为，连接并延长交于点，连接，过点作交的延长线于点，连接．

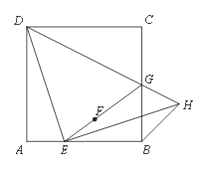
（1）求证：；

（2）用等式表示线段与的数量关系，并证明．

（3）若正方形的边长为4，取DH的中点M，请直接写出线段BM长的最小值。

Answer 1

【答案】（1）详见解析；（2），证明详见解析；（3）BM最小值为

【解析】

（1）连接．首先证明，再证≌，即可得证；

（2）首先在上取点使得，连接，由（1）中≌，得出，同理可得，进而得出∠EDG=45°，然后根据

得出DE=HE，又由AD=AB，AM=AE，得出DM=EB，再由余角的性质得∠MDE=∠BEH进而判定≌，得出，在中，利用勾股定理，得，即可得出；

（3）将正方形看成以点A为原点的坐标系，设AE=x，根据题意，得出，即点M在线段AC上，当BM⊥AC时，BM最小，即可得解.

（1）证明：连接．

∵点关于直线的对称点为，

∴DA=DF，EA=EF

又∵DE=DE

∴（SSS）

∴∠DFE=90°

又∵DA=DF，DA=DC

∴DF=DC

又∵DG=DG

∴≌（HL）

∴．

（2）．

证明：在上取点使得，连接．

∵≌

∴

同理：

∴

又∵

∴DE=HE

又∵AD=AB，AM=AE

∴DM=EB

又∵∠MDE+∠AED=∠BEH+∠AED=90°

∴∠MDE=∠BEH

∴≌（SAS）.

∴

在中，，．

∴

即.

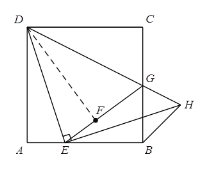
（3）将正方形看成以点A为原点的坐标系，如图所示，

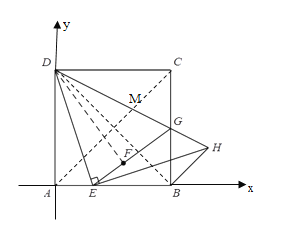
设AE=x

根据题意，得A（0,0），D（0,4），

是边上的一动点，由（2）得知，则H（x+4，x）

∵DH的中点M，由中点坐标公式，得

∴

∴点M在线段AC上，

∴当BM⊥AC时，BM最小，BM最小值为