ЬтФПФкШн
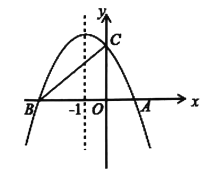
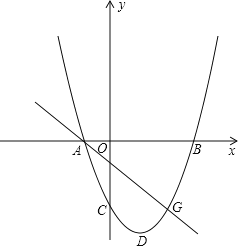
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЌгыyжсИКАыжсНЛгкCЕуЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЦфжаBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌЧвOBЃНOCЃЎ
ЃЌгыyжсИКАыжсНЛгкCЕуЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЦфжаBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌЧвOBЃНOCЃЎ
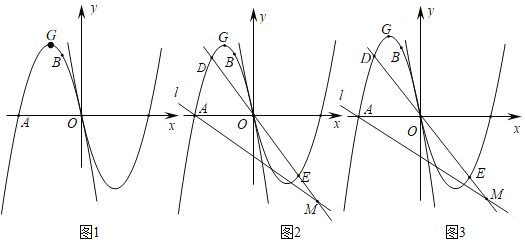
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуGЃЈ2ЃЌyЃЉЪЧИУХзЮяЯпЩЯвЛЕуЃЌЕуPЪЧжБЯпAGЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїAPGЕФУцЛ§зюДѓЃПЧѓГіДЫЪБPЕуЕФзјБъКЭЁїAPGЕФзюДѓУцЛ§.
ЃЈ3ЃЉШєЦНаагкxжсЕФжБЯпгыИУХзЮяЯпНЛгкMЁЂNСНЕуЃЈЦфжаЕуMдкЕуNЕФгвВрЃЉЃЌдкxжсЩЯЪЧЗёДцдкЕуQЃЌЪЙЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉPЕуЕФзјБъЮЊ
ЃЛЃЈ2ЃЉPЕуЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉQЃЈЃ
ЃЛЃЈ3ЃЉQЃЈЃ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌИљОнвбжЊЕУЕНCЃЈ0ЃЌЉ3ЃЉЃЌAЃЈЉ1ЃЌ0ЃЉЃЌДњШыЕУЕНЗНГЬзщ
ЃЌИљОнвбжЊЕУЕНCЃЈ0ЃЌЉ3ЃЉЃЌAЃЈЉ1ЃЌ0ЃЉЃЌДњШыЕУЕНЗНГЬзщ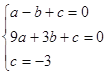 ЃЌЧѓГіЗНГЬзщЕФНтМДПЩЃЛ
ЃЌЧѓГіЗНГЬзщЕФНтМДПЩЃЛ
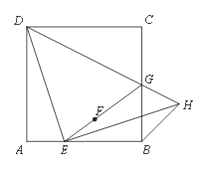
ЃЈ2ЃЉЙ§ЕуPзїyжсЕФЦНааЯпгыAGНЛгкЕуFЃЌЧѓГіЕуGЕФзјБъЃЈ2ЃЌЉ3ЃЉЃЌЩшжБЯпAGЮЊ![]() ЃЌДњШыЕУЕН
ЃЌДњШыЕУЕН![]() ЃЌЧѓГіЗНГЬзщЕФНтЕУГіжБЯпAGЮЊ
ЃЌЧѓГіЗНГЬзщЕФНтЕУГіжБЯпAGЮЊ![]() ЃЌЩшPЃЈxЃЌ
ЃЌЩшPЃЈxЃЌ![]() ЃЉЃЌдђFЃЈxЃЌЉxЉ1ЃЉЃЌPF
ЃЉЃЌдђFЃЈxЃЌЉxЉ1ЃЉЃЌPF![]() ЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЧѓГіЁїAPGЕФУцЛ§ЃЌЛЏГЩЖЅЕуЪНМДПЩЃЛ
ЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЧѓГіЁїAPGЕФУцЛ§ЃЌЛЏГЩЖЅЕуЪНМДПЩЃЛ
ЃЈ3ЃЉДцдкЃЎИљОнMNЁЮxжсЃЌЧвMЁЂNдкХзЮяЯпЩЯЃЌЕУЕНMЁЂNЙигкжБЯпx=1ЖдГЦЃЌЩшЕуMЮЊЃЈmЃЌ![]() ЃЉЧвmЃО1ЃЌЕУЕНMN=2ЃЈmЉ1ЃЉЃЌЕБЁЯQMN=90ЁуЃЌЧвMN=MQЪБЃЌгЩЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌЕУЕН
ЃЉЧвmЃО1ЃЌЕУЕНMN=2ЃЈmЉ1ЃЉЃЌЕБЁЯQMN=90ЁуЃЌЧвMN=MQЪБЃЌгЩЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌЕУЕН![]() ЃЌЧѓГіmЕФжЕЃЌЕУГіЕуMКЭЕуQЕФзјБъЃЛЕБЁЯQNM=90ЁуЃЌЧвMN=NQЪБЃЌЭЌРэПЩЧѓЕуQЕФзјБъЃЌЕБЁЯNQM=90ЁуЃЌЧвMQ=NQЪБЃЌЙ§QзїQEЁЭMNгкЕуEЃЌдђQE=
ЃЌЧѓГіmЕФжЕЃЌЕУГіЕуMКЭЕуQЕФзјБъЃЛЕБЁЯQNM=90ЁуЃЌЧвMN=NQЪБЃЌЭЌРэПЩЧѓЕуQЕФзјБъЃЌЕБЁЯNQM=90ЁуЃЌЧвMQ=NQЪБЃЌЙ§QзїQEЁЭMNгкЕуEЃЌдђQE=![]() MNЃЌИљОнХзЮяЯпМАЕШбќжБНЧШ§НЧаЮЕФжсЖдГЦадЃЌЕУЕНЕуQЕФзјБъЃЎ
MNЃЌИљОнХзЮяЯпМАЕШбќжБНЧШ§НЧаЮЕФжсЖдГЦадЃЌЕУЕНЕуQЕФзјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
гЩвбжЊЕУЃКCЃЈ0ЃЌЉ3ЃЉЃЌAЃЈЉ1ЃЌ0ЃЉЃЌ
Ёр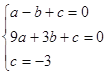 ЃЌНтЕУ
ЃЌНтЕУ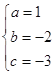 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§ЕуPзїyжсЕФЦНааЯпгыAGНЛгкЕуQЃЌ
гЩ![]() ЃЌСюx=2ЃЌдђy=Ѓ3ЃЌЁрЕуGЮЊЃЈ2ЃЌЃ3ЃЉЃЌ
ЃЌСюx=2ЃЌдђy=Ѓ3ЃЌЁрЕуGЮЊЃЈ2ЃЌЃ3ЃЉЃЌ
ЩшжБЯпAGЮЊ![]() ЃЌЁр
ЃЌЁр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌМДжБЯпAGЮЊ
ЃЌМДжБЯпAGЮЊ![]() ЃЌ
ЃЌ
ЩшPЃЈxЃЌ![]() ЃЉЃЌдђFЃЈxЃЌЃxЃ1ЃЉЃЌPF
ЃЉЃЌдђFЃЈxЃЌЃxЃ1ЃЉЃЌPF![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌЁїAPGЕФУцЛ§зюДѓЃЌДЫЪБPЕуЕФзјБъЮЊ
ЪБЃЌЁїAPGЕФУцЛ§зюДѓЃЌДЫЪБPЕуЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ЃЈ3ЃЉДцдкЃЎ
ЁпMNЁЮxжсЃЌЧвMЁЂNдкХзЮяЯпЩЯЃЌЁрMЁЂNЙигкжБЯпx=1ЖдГЦЃЌ
ЩшЕуMЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЧв
ЃЉЧв![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЕБЁЯQMN=90ЁуЃЌЧвMN=MQЪБЃЌЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌЁрMQЁЭMNМДMQЁЭxжсЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() Лђ
Лђ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсЃЉЛђ
ЃЈЩсЃЉЛђ![]() ЃЌ
ЃЌ![]() ЃЈЩсЃЉЃЌ
ЃЈЩсЃЉЃЌ
ЁрЕуMЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЁрЕуQЮЊЃЈ
ЃЉЃЌЁрЕуQЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЕБЁЯQNM=90ЁуЃЌЧвMN=NQЪБЃЌЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌЭЌРэПЩЧѓЕуQЮЊЃЈЃ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЕБЁЯNQM=90ЁуЃЌЧвMQ=NQЪБЃЌЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌ
Й§QзїQEЁЭMNгкЕуEЃЌдђQE=![]() MNЃЌ
MNЃЌ![]() ЃЌ
ЃЌ
ЁпЗНГЬгаНтЃЌЁргЩХзЮяЯпМАЕШбќжБНЧШ§НЧаЮЕФжсЖдГЦаджЊЕуQЮЊЃЈ1ЃЌ0ЃЉЃЌ
злЩЯЫљЪіЃЌТњзуДцдкТњзуЬѕМўЕФЕуQЃЌЗжБ№ЮЊЃЈЃ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
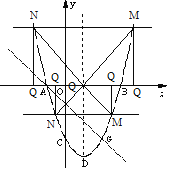

 УћЪІЕуВІОэЯЕСаД№АИ
УћЪІЕуВІОэЯЕСаД№АИ