题目内容
10.在矩形ABCD中,将对角线CA绕点C逆时针旋转得到CE,连接AE,取AE的中点F,连接BF,DF.(1)若点E在CB的延长线上,如图1.
①依题意补全图1;
②判断BF与DF的位置关系并加以证明;
(2)若点E在线段BC的下方,如果∠ACE=90°,∠ACB=28°,AC=6,请写出求BF长的思路.(可以不写出计算结果)
分析 (1)由题意,补全图形,如图1,
(2)由矩形的性质,得到△AFD≌△EFG,再用等量代换即可;
(3)先计算出∠BAC,∠AOB,在求出∠BOF,∠BDF,最后利用三角函数计算即可.
解答 解:(1)①补全图形,如图1,所示,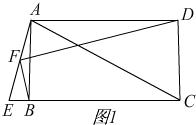
②BF⊥DF.
证明:延长DF与CE的延长线交于点G,如图2,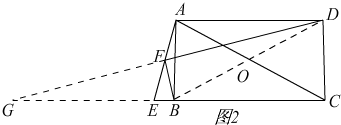
连接BD,
∵矩形ABCD中,AD∥BC,AD=BC,AC=BD,
∴∠ADF=∠G,
在△AFD和△EFG中,
$\left\{\begin{array}{l}{∠AFD=∠EFG}\\{∠ADF=∠G}\\{AF=EF}\end{array}\right.$,
∴△AFD≌△EFG,
∴EG=AD,GF=DF,
∴EG=BC,
∴BG=EC,
∴BG=BD,
∵GF=DF,
∴BF⊥DF;
(2)如图3,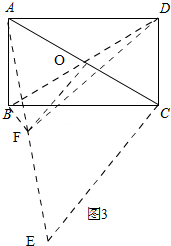
由(2)有,BF⊥DF,
在矩形ABCD中,
∵∠ACB=28°,
∴∠BAC=90°-∠ACB=62°,∠AOB=2∠ACB=56°,
∵OA=OC,AF=EF,
∴OF∥EC,
∴∠AOF=∠ACB=28°,
∴∠BOF=∠AOB-∠AOF=28°,
在Rt△BFD中,OB=OD,
∴OF=OD,
∴∠BDF=$\frac{1}{2}$∠BOF=14°,
在Rt△BFD中,BD=AC=6,
sin∠BDF=$\frac{BF}{BD}$,
∴BF=BD×sin∠BDF=6sin14°≈6×0.24192190≈1.452.
点评 此题是四边形综合题,主要考查了全等三角形的性质和判定,等腰三角形的性质,锐角三角函数,推导出∠BDF是解本题的关键.

练习册系列答案
相关题目
15.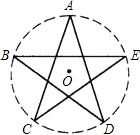 如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
 如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )| A. | a•sin72° | B. | $\frac{a}{tan72°}$ | C. | $\frac{a}{cos18°}$ | D. | $\frac{a}{cos36°}$ |
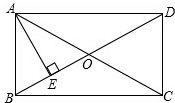 在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD,垂足为E,且AE平分∠BAO.若DO=2,求AB和BC的长度.
在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD,垂足为E,且AE平分∠BAO.若DO=2,求AB和BC的长度. 如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.
如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.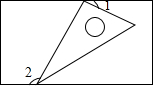 如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°.
如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°.