题目内容
13.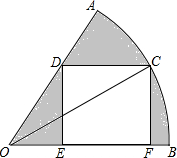 如图,在扇形AOB中,∠AOB=60°,A0O=6,OC平分∠AOB,交$\widehat{AB}$于C,CF⊥OB于F,CD∥OB,交OA于D,DE⊥OB于E.求图中阴影部分的面积.
如图,在扇形AOB中,∠AOB=60°,A0O=6,OC平分∠AOB,交$\widehat{AB}$于C,CF⊥OB于F,CD∥OB,交OA于D,DE⊥OB于E.求图中阴影部分的面积.
分析 由OC平分∠AOB,得到∠COB=30°,根据直角三角形的性质得到CF=$\frac{1}{2}$OC=$\frac{1}{2}$OA=3,推出四边形DEFC是矩形,证得矩形DEFC是正方形,然后根据图形的面积即可得到结论.
解答 解:∵ ∠AOB=60°,OC平分∠AOB,
∠AOB=60°,OC平分∠AOB,
∴∠COB=30°,
∵CF⊥OB于F,
∴∠CFO=90°,
∴CF=$\frac{1}{2}$OC=$\frac{1}{2}$OA=3,
∵CF⊥OB,DE⊥OB,
∴DE∥CF,
∵CD∥OB,
∴四边形DEFC是矩形,∠DCO=∠COB=30°,
∴DE=CF=3,∠DOC=30°,
∵DE=$\frac{\sqrt{3}}{2}$OD,
∴OD=3,
∴CD=DE=3,
∴矩形DEFC是正方形,
∴S阴影=S扇形AOB-S正方形=$\frac{60•π×{6}^{2}}{360}$-3×3=6π-9.
点评 本题考查了扇形的面积的计算,正方形的判定和性质,直角三角形的性质,正确的识别图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 矩形ABCD中,M是AD的中点,N是BC的中点,点P是CD的延长线连接PM延长交AC于点Q,连接PN,QN.
矩形ABCD中,M是AD的中点,N是BC的中点,点P是CD的延长线连接PM延长交AC于点Q,连接PN,QN.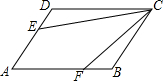 如图,在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF=$\frac{263}{24}$cm.
如图,在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF=$\frac{263}{24}$cm.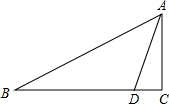 如图,在△ABC中,∠C=90°,D是BC边上一点,∠BAD=45°,AC=3,BD=5,求AB的长.
如图,在△ABC中,∠C=90°,D是BC边上一点,∠BAD=45°,AC=3,BD=5,求AB的长. 如图所示,比较a,b,-a,-b的大小:a<-b<b<-a.
如图所示,比较a,b,-a,-b的大小:a<-b<b<-a. 如图,A、B、C是⊙O上三点,∠AOB的度数是50°,∠OBC=40°,则∠OAC是25°.
如图,A、B、C是⊙O上三点,∠AOB的度数是50°,∠OBC=40°,则∠OAC是25°.