题目内容
1.在学习中,小明发现:当n=0,1,2时,n2-3n-2的值都是负数,于是小明猜想:当n为任意自然数时,n2-3n-2的值都是负数,小明的猜想正确吗?请说明理由.分析 先将n2-3n-2配方,再计算其有没有可能为正数.
解答 解:小明的猜想不正确,理由是:
n2-3n-2,
=n2-3n+($\frac{3}{2}$)2-($\frac{3}{2}$)2-2,
=(n-$\frac{3}{2}$)2-$\frac{17}{4}$,
∴当(n-$\frac{3}{2}$)2>$\frac{17}{4}$时,n2-3n-2的值就是正数,比如当n=4时,n2-3n-2=(4-$\frac{3}{2}$)2-$\frac{17}{4}$=2>0,
所以n2-3n-2的值可能是负数,也可能是正数,
所以小明的猜想不正确.
点评 本题考查了配方法的应用,将一个代数式配方时,先将二次项系数化为1,然后在式子上加上一次项系数一半的平方,再减去相同的式子,进行配方;利用配方法还可以证明一个代数式为一个非负数.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
6.与$\frac{1}{4}$:$\frac{1}{5}$能组成比例的是( )
| A. | $\frac{1}{5}$:$\frac{1}{4}$ | B. | $\frac{1}{10}$:$\frac{1}{8}$ | C. | $\frac{1}{8}$:$\frac{1}{10}$ | D. | $\frac{1}{8}$:$\frac{1}{5}$ |
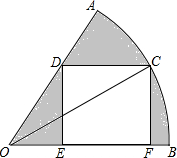 如图,在扇形AOB中,∠AOB=60°,A0O=6,OC平分∠AOB,交$\widehat{AB}$于C,CF⊥OB于F,CD∥OB,交OA于D,DE⊥OB于E.求图中阴影部分的面积.
如图,在扇形AOB中,∠AOB=60°,A0O=6,OC平分∠AOB,交$\widehat{AB}$于C,CF⊥OB于F,CD∥OB,交OA于D,DE⊥OB于E.求图中阴影部分的面积.